《2025年一本初中数学应用题》

1.甲、乙两名运动员在周长为 200 m 的圆形跑道上训练,两人从同一处同时同向出发,甲的跑步速度为5 m/s,乙的跑步速度为3 m/s,两人第 3 次相遇时,经过( )

A.200 s
B.300 s
C.400 s
D.500 s

答案： B 【解析】设经过x s两人第3次相遇.
由题意,得5x-3x=200×3,解得x=300.

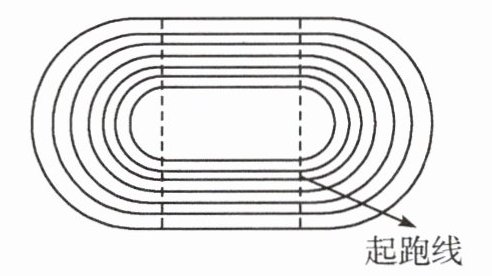
2.某校根据国际田联标准和学校场地的实际情况规划运动会比赛场地,第一分道实跑线长为400 m,第二分道实跑线长为 407 m,第三分道实跑线长为 415 m,小军沿着第一分道实跑线逆时针跑步,王教练沿着第二分道实跑线顺时针骑自行车,两人从图中起跑线的位置同时出发,经过 20 s 两人在直道第一次相遇.王教练骑自行车的平均速度是小军跑步的平均速度的2倍,则小军跑步的平均速度是______m/s.
(注:在同侧直道,过两人所在点的直线与直跑道边线垂直时,称两人直道相遇)

起跑线

答案： 6.725 【解析】设小军跑步的平均速度是x m/s,则王教练骑自行车的平均速度是2x m/s.
由题意,得20x+20×2x=400+$\frac{407-400}{2}$,
解得x=6.725,
∴小军跑步的平均速度是6.725 m/s.

3.某人下午6点多外出时,看手表两指针的夹角为110°,下午7点前回家发现两指针的夹角仍为110°,则他外出的时间为______min.

答案： 40 【解析】设他外出的时间为x min.
分针每分钟转360°÷60=6°,
时针每分钟转30°÷60=0.5°.
由题意,得6x=110+110+0.5x,解得x=40,
∴他外出的时间为40 min.

4.甲、乙两人在周长为 400 m 的环形操场上练习跑步,甲每分钟跑 180 m.
(1)若两人从同一起点同时反向而行,1.25 min后第一次相遇,则乙每分钟跑多少米?
(2)若两人从同一起点同时同向而行,5 min后第一次相遇,则乙每分钟跑多少米?

答案： 4.解:
(1)设乙每分钟跑x m.
由题意,得(180+x)×1.25=400,解得x=140.
答:乙每分钟跑140 m.
(2)设乙每分钟跑y m.
当乙比甲快时,有(y-180)×5=400,解得y=260;
当甲比乙快时,有(180-y)×5=400,解得y=100.
答:乙每分钟跑260 m或100 m.

5.甲、乙两人在环形跑道上练习跑步,已知环形跑道的周长为400 m,乙每秒跑6 m,甲的速度是乙速度的$\frac{4}{3}$.
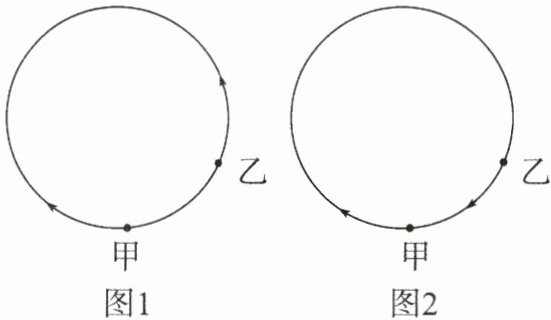
(1)如图1,如果甲、乙两人在跑道上相距8 m处同时反向出发,那么经过多少秒,甲、乙两人首次相遇?
(2)如图2,如果甲在乙前面8 m处与乙同时同向出发,那么经过多少秒,甲、乙两人首次相遇?

答案： 5.解:
(1)设经过x s,甲、乙两人首次相遇.
由题意,得6×$\frac{4}{3}$x+6x=400-8,
解得x=28.
答:经过28 s,甲、乙两人首次相遇.
(2)设经过y s,甲、乙两人首次相遇.
由题意,得6×$\frac{4}{3}$y=6y+400-8,解得y=196.
答:经过196 s,甲、乙两人首次相遇.
【注意】问题中的等量关系:
(1)相遇问题;
(2)追及问题.