《2025年超越训练八年级数学上册人教版四川专版》

13. 分解因式:$xy - 1 + x - y = $.

答案： $(x - 1)(y + 1)$

14. 如果方程$\frac{x - 3}{x - 2} + 1 = \frac{m}{x - 2}$有增根,那么$m$的值为.

答案： $-1$（或 填对应选项）

15. 已知$a + b = \frac{7}{5}$,$ab = \frac{12}{25}$,则$a^2 + b^2$的值为.

答案： $1$

16. 如图,在$\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AB = AC$,$D$是$AC$边的中点,$CE \perp BD$,交$BD$的延长线于点$E$,交$BA$的延长线于点$F$.若$BF = 12$,则$\triangle FBC$的面积为.

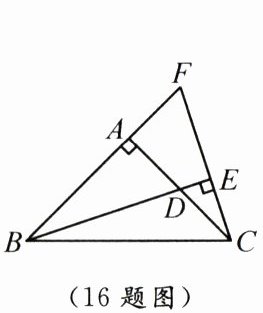
答案： 【解析】：设AD=DC=x，则AC=AB=2x。
∵∠BAC=90°，F在BA延长线上，
∴∠CAF=90°。
∵CE⊥BD，
∴∠BEC=90°，则∠ABD+∠ADB=90°，∠ACF+∠CDE=90°。
∵∠ADB=∠CDE（对顶角），
∴∠ABD=∠ACF。
在△ABD和△ACF中，∠ABD=∠ACF，AB=AC，∠BAD=∠CAF=90°，
∴△ABD≌△ACF（ASA），
∴AD=AF=x。
∵BF=BA+AF=2x+x=3x=12，
∴x=4，AC=AB=8。
△FBC面积=1/2×BF×AC=1/2×12×8=48。
【答案】：48

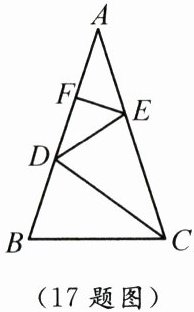
17. 如图,在$\triangle ABC$中,$D$,$F$为$AB$上的点,$E$为$AC$上的点,其中$B$,$E$两点关于直线$CD$对称,$A$,$D$两点关于直线$EF$对称.若$AB = AC = m$,$BC = n$,则下列结论正确的是(填序号).
①$BD = m - n$;②$2m = 3n$;③$EF = \frac{n}{2}$;④$AE = 2n - m$;⑤$CD = n$.

答案： ①

18. 已知$A(0,4)$,$B(3,0)$,$C(a,b)$为平面直角坐标系内的点.若$\angle ABC = 90^{\circ}$,$BA = BC$,则$ab$的值为.

答案： 21或3

19. (8分)解答下列各题:
(1)计算:$(x + 1)(x - 2) - (x - 2)(x + 2)$;
(2)解方程:$\frac{1}{3(3x - 1)} - \frac{x}{3x - 1} = \frac{2}{3}$.

答案：
(1)
$(x + 1)(x - 2) - (x - 2)(x + 2)$
$=(x^2 - 2x + x - 2) - (x^2 - 4)$
$=x^2 - x - 2 - x^2 + 4$
$=2 - x$
(2)
$\frac{1}{3(3x - 1)} - \frac{x}{3x - 1}$
$=\frac{1}{3(3x - 1)} - \frac{3x}{3(3x - 1)}$
$=\frac{1 - 3x}{3(3x - 1)}$
$=\frac{-(3x - 1)}{3(3x - 1)}$
$=-\frac{1}{3}$
则原方程$\frac{1}{3(3x - 1)} - \frac{x}{3x - 1} = \frac{2}{3}$可化为$-\frac{1}{3}=\frac{2}{3}$（矛盾）或$3x-1 = 0$（分式方程分母不为$0$，此情况舍去）情况不成立，我们重新整理方程：
方程两边同乘$3(3x - 1)$得：
$1 - 3x = 2(3x - 1)×1$
$1 - 3x = 6x - 2$
$-3x - 6x = -2 - 1$
$-9x = -3$
$x = \frac{1}{3}$
检验：当$x = \frac{1}{3}$时，$3(3x - 1)=3×(3×\frac{1}{3}-1)=0$，
所以$x = \frac{1}{3}$是增根，原方程无解。