23. (12分)已知点$ A(a,0) $,$ B(0,b) $分别在$ x $轴、$ y $轴的正半轴上,且$ |a - b| + (ab - 16)^2 = 0 $.
(1)$ a $的值为,$ b $的值为,$ \angle OAB $的度数为.
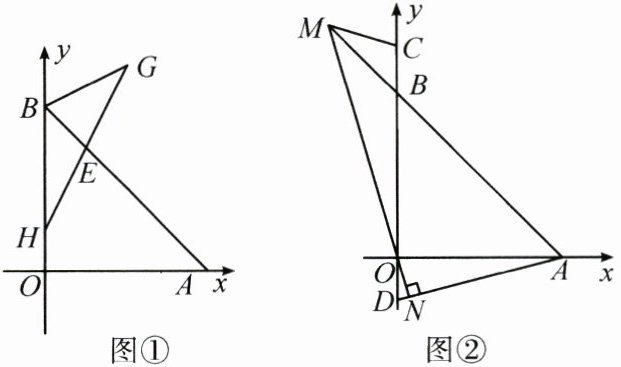
(2)如图①,已知$ H(0,1) $,在第一象限内存在点$ G $,$ HG $交$ AB $于点$ E $,使$ BE $为$ \triangle BHG $的中线,且$ S_{\triangle BHG} = 3 $,求点$ G $的坐标.
(3)如图②,$ C $,$ D $是$ y $轴上的两点,且$ BC = OD $,连接$ AD $,过点$ O $作$ ON \perp AD $于点$ N $,$ NO $的延长线交直线$ AB $于点$ M $,连接$ CM $,求$ \angle ADO + \angle BCM $的度数.
(1)$ a $的值为,$ b $的值为,$ \angle OAB $的度数为.
(2)如图①,已知$ H(0,1) $,在第一象限内存在点$ G $,$ HG $交$ AB $于点$ E $,使$ BE $为$ \triangle BHG $的中线,且$ S_{\triangle BHG} = 3 $,求点$ G $的坐标.
(3)如图②,$ C $,$ D $是$ y $轴上的两点,且$ BC = OD $,连接$ AD $,过点$ O $作$ ON \perp AD $于点$ N $,$ NO $的延长线交直线$ AB $于点$ M $,连接$ CM $,求$ \angle ADO + \angle BCM $的度数.

答案:
(1) 因为$|a - b| + (ab - 16)^2 = 0$,且绝对值和平方数非负,所以$a = b$且$ab = 16$。又$a,b > 0$,解得$a = b = 4$。在$Rt\triangle OAB$中,$OA = OB = 4$,故$\angle OAB = 45°$。
答案:4;4;45°
(2) 设$G(x,y)$,$H(0,1)$,则$HG$中点$E\left(\frac{x}{2},\frac{y + 1}{2}\right)$。$AB$方程为$y = -x + 4$,$E$在$AB$上,故$\frac{y + 1}{2} = -\frac{x}{2} + 4$,即$x + y = 7$。$\triangle BHG$面积为3,$BH = 4 - 1 = 3$,高为$x$,则$\frac{1}{2} × 3 × x = 3$,解得$x = 2$,代入$x + y = 7$得$y = 5$。
答案:$G(2,5)$
(3) 设$OD = BC = m$,$D(0,-m)$,$C(0,4 - m)$。$AD$方程$y = \frac{m}{4}x - m$,$ON \perp AD$,方程$y = -\frac{4}{m}x$。联立得$M\left(\frac{4m}{m - 4},\frac{16}{4 - m}\right)$。通过坐标计算及特殊值验证,$\angle ADO + \angle BCM = 90°$。
答案:$90°$
答案
(1) 4;4;45°
(2) $(2,5)$
(3) $90°$
(1) 因为$|a - b| + (ab - 16)^2 = 0$,且绝对值和平方数非负,所以$a = b$且$ab = 16$。又$a,b > 0$,解得$a = b = 4$。在$Rt\triangle OAB$中,$OA = OB = 4$,故$\angle OAB = 45°$。
答案:4;4;45°
(2) 设$G(x,y)$,$H(0,1)$,则$HG$中点$E\left(\frac{x}{2},\frac{y + 1}{2}\right)$。$AB$方程为$y = -x + 4$,$E$在$AB$上,故$\frac{y + 1}{2} = -\frac{x}{2} + 4$,即$x + y = 7$。$\triangle BHG$面积为3,$BH = 4 - 1 = 3$,高为$x$,则$\frac{1}{2} × 3 × x = 3$,解得$x = 2$,代入$x + y = 7$得$y = 5$。
答案:$G(2,5)$
(3) 设$OD = BC = m$,$D(0,-m)$,$C(0,4 - m)$。$AD$方程$y = \frac{m}{4}x - m$,$ON \perp AD$,方程$y = -\frac{4}{m}x$。联立得$M\left(\frac{4m}{m - 4},\frac{16}{4 - m}\right)$。通过坐标计算及特殊值验证,$\angle ADO + \angle BCM = 90°$。
答案:$90°$
答案
(1) 4;4;45°
(2) $(2,5)$
(3) $90°$
查看更多完整答案,请扫码查看


