《2025年超越训练八年级数学上册人教版四川专版》

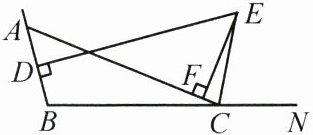
22. （8分）如图，$CE$是$\triangle ABC$的外角$\angle ACN$的平分线，$DE$垂直平分$AB$，$EF\perp AC$于点$F$.若$AF = 10$，$CF = 1$，求$BC$的长.

答案：

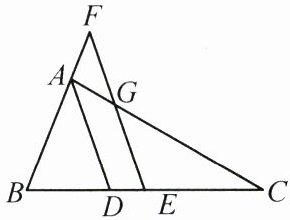
23. （8分）如图，$AD$为$\triangle ABC$的角平分线，$E$为$BC$的中点，$EF// AD$交$BA$的延长线于点$F$，交$AC$于点$G$.
（1）求证：$BF = CG$；
（2）求$\frac{AB + AC}{CG}$的值.

答案： （1）证明：过点$ C $作$ CH // AB $交$ FE $的延长线于点$ H $。
∵$ E $为$ BC $中点，
∴$ BE=CE $。
∵$ CH // AB $，
∴$ \angle F=\angle H $（两直线平行，内错角相等）。
在$ \triangle BEF $和$ \triangle CEH $中，
$ \begin{cases} \angle F=\angle H \\ \angle BEF=\angle CEH \\ BE=CE \end{cases} $，
∴$ \triangle BEF \cong \triangle CEH $（AAS），
∴$ BF=CH $。
∵$ EF // AD $，
∴$ \angle F=\angle BAD $（同位角相等），$ \angle AGF=\angle CAD $（内错角相等）。
∵$ AD $平分$ \angle BAC $，
∴$ \angle BAD=\angle CAD $，
∴$ \angle F=\angle AGF $，
∴$ AF=AG $（等角对等边）。
∵$ CH // AB $，
∴$ \angle H=\angle F $，又$ \angle HGC=\angle AGF $（对顶角相等），
∴$ \angle H=\angle HGC $，
∴$ CH=CG $（等角对等边）。
∵$ BF=CH $，
∴$ BF=CG $。
（2）
∵$ BF=AB+AF $，且$ BF=CG $，
∴$ CG=AB+AF $。
∵$ AG+CG=AC $，
∴$ AG=AC-CG $。
∵$ AF=AG $，
∴$ AF=AC-CG $。
∴$ CG=AB+(AC-CG) $，整理得$ 2CG=AB+AC $，
∴$ \frac{AB+AC}{CG}=2 $。
答案：（1）见证明过程；（2）$ 2 $。