《2025年超越训练八年级数学上册人教版四川专版》

12. 若一个三角形两边的长分别为2，7，且第三边的长为偶数，则此三角形的周长是.

答案： 15或17

13. 如图，已知$ \angle B = \angle ADB $，$ \angle DAC = 15^{\circ} $，$ \angle C = 20^{\circ} $，则$ \angle EAC $的度数是.

答案： 55°

14. 如图，AD是△ABC的中线，$ DH \perp AB $，垂足为H，$ DG \perp AC $，垂足为G，$ AB = 7 $，$ AC = 6 $，$ DH = 3 $，则DG的长是.

答案： 3.5

15. 如图，在Rt△ABC中，$ \angle C = 90^{\circ} $，BD是角平分线，E是AD上一点，过点E作$ FH \perp AB $，垂足为H，交BD的延长线于点F.若$ \angle F = 54^{\circ} $，则$ \angle FED $的度数是.

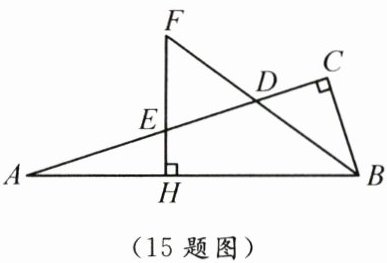
答案：

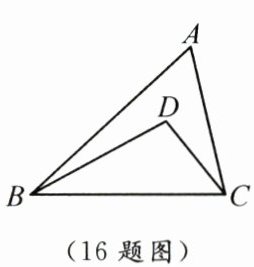
16. 如图，D是△ABC内一点，$ \angle ABD = \frac{1}{3}\angle ABC $，$ \angle ACD = \frac{1}{3}\angle ACB $.若$ \angle A = \alpha $，则$ \angle BDC = $(用含α的代数式表示).

答案： 60° + $\frac{2}{3}\alpha$

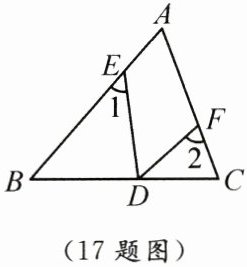
17. 如图，在△ABC中，$ \angle A = 62^{\circ} $，E，D，F分别是边AB，BC，AC上的点.若$ \angle 1 = \angle B $，$ \angle 2 = \angle C $，则$ \angle EDF $的度数是.

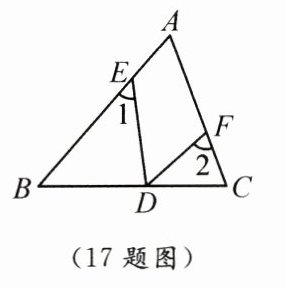
答案： 1. 首先，根据三角形内角和定理：
在$\triangle ABC$中，$\angle A+\angle B + \angle C=180^{\circ}$，已知$\angle A = 62^{\circ}$，则$\angle B+\angle C=180^{\circ}-\angle A$。
把$\angle A = 62^{\circ}$代入可得$\angle B+\angle C=180 - 62=118^{\circ}$。
2. 然后，根据平角的定义：
因为$\angle 1+\angle EDF+\angle 2 = 180^{\circ}$（平角的度数为$180^{\circ}$），又已知$\angle 1=\angle B$，$\angle 2=\angle C$。
所以$\angle EDF=180^{\circ}-(\angle 1 + \angle 2)$。
由于$\angle 1+\angle 2=\angle B+\angle C$。
3. 最后，得出$\angle EDF$的度数：
把$\angle B+\angle C = 118^{\circ}$代入$\angle EDF=180^{\circ}-(\angle 1 + \angle 2)$中，可得$\angle EDF = 62^{\circ}$。
故答案为$62^{\circ}$。

18. 如图，在△ABC中，$ \angle B = 33^{\circ} $，将△ABC沿直线EF翻折，使点B落在点D处，则$ \angle 1 - \angle 2 $的度数是.

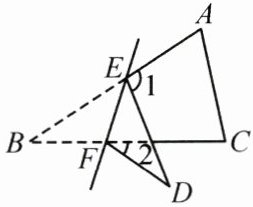
答案：

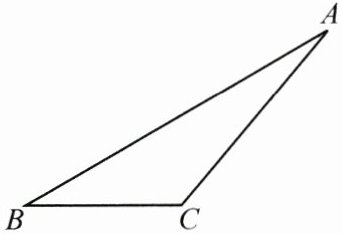
19. （8分）如图，已知△ABC.
（1）作出△ABC的角平分线AE和边BC上的高AD；
（2）若$ \angle B = 30^{\circ} $，$ \angle ACB = 130^{\circ} $，求$ \angle EAD $的度数.

答案：