《2025年超越训练八年级数学上册人教版四川专版》

10. 若式子$x^{2}+2(m-3)x+1$是完全平方式，$x+n$与$x+2$的乘积的展开式中不含$x$的一次项，则$n^{m}$的值是()

A.$-4$
B.$16$
C.$-4$或$-16$
D.$4$或$16$

答案： D

11. 如果一个数等于两个连续奇数的平方差，那么我们称这个数为“幸福数”.下列数为“幸福数”的是()

A.$205$
B.$250$
C.$502$
D.$520$

答案： D

12. 如图，将一边长为$a$的正方形与四块边长为$b$的正方形(其中$b＞a$)拼接在一起，则四边形$ABCD$的面积是()


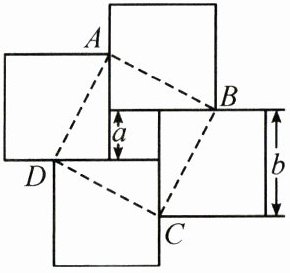
A.$b^{2}+(b-a)^{2}$
B.$b^{2}+a^{2}$
C.$(b+a)^{2}$
D.$a^{2}+2ab$

答案：

13. 若$3^{x}=729$，$9^{y}=81$，则$3^{x-2y}=$.

答案： 9

14. 分解因式：$12x^{2}y-3y^{3}=$.

答案： $3y(2x + y)(2x - y)$。

15. 若实数$x$，$y$满足方程组$\begin{cases}x - y = - \frac{1}{2}, \\ 2x + 2y = 5\end{cases}$，则$x^{2}-y^{2}$的值为.

答案： $-\frac{5}{4}$（或填$-1.25$）

16. 若$m-n=2$，$mn=-1$，则代数式$(1-2m)(1-2n)$的值为.

答案： -3

17. 已知$x=3y+5$，且$x^{2}-7xy+9y^{2}=24$，则$x^{2}y-3xy^{2}$的值为.

答案： 5

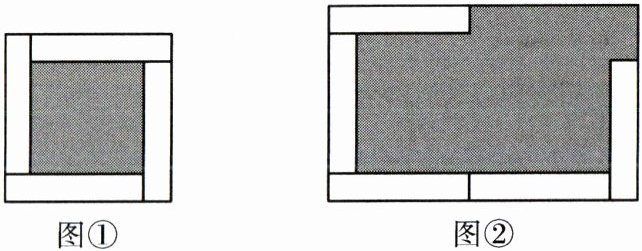
18. 图①是由4个相同的白色的长方形和1个灰色的正方形构成的正方形，图②是由5个白色的长方形(每个长方形的大小和图①中的相同)和1个灰色的不规则图形构成的长方形.已知图①、图②中灰色图形的面积分别为144和468，则每个白色长方形的面积为.

答案： 【解析】：设每个白色长方形的长为$a$，宽为$b$。
由图①（大正方形）：中间灰色小正方形边长为$a - b$，面积$(a - b)^2 = 144$，则$a - b = 12$①。
大正方形边长为$a + b$，面积$(a + b)^2 = 4ab + 144$。
由图②（长方形）：总面积为$5ab + 468$。设长方形长为$a + b$，宽为$a + 2b$（或长$a + 2b$，宽$a + b$），则面积$(a + b)(a + 2b) = 5ab + 468$②。
将$a = b + 12$代入②：
$(b + 12 + b)(b + 12 + 2b) = 5(b + 12)b + 468$
$(2b + 12)(3b + 12) = 5b^2 + 60b + 468$
$6b^2 + 60b + 144 = 5b^2 + 60b + 468$
解得$b^2 = 324$，$b = 18$（$b ＞ 0$）。
则$a = 18 + 12 = 30$，长方形面积$ab = 30×18 = 540$。
【答案】：540