《2025年实验班提优训练四年级数学上册苏教版》

1. 桌子上放着分别写有1～15数的卡片,小明和小芳两人玩摸牌游戏,规则如下:如果摸出的是2的整数倍,那么小明赢;如果摸出的不是2的整数倍,那么小芳赢。
(1)这个游戏规则公平吗?为什么?
(2)小明一定会输吗?
(3)请你设计一个公平的游戏规则。

答案： 1.
(1)不公平,因为摸出2的整数倍的可能性和摸出不是2的整数倍的可能性不相等,所以这个游戏规则不公平。
(2)虽然小明赢的可能性比小芳小,但是小明不一定会输,只是相对而言,小明输的可能性要大一些。
(3)添加一张写有“16”的卡片。(答案不唯一)[提示]
(1)判断游戏规则是否公平,要看每个人赢的可能性是否相等。1~15这15个数中,是2的整数倍的有2、4、6、8、10、12、14,共7个数;不是2的整数倍的有1、3、5、7、9、11、13、15,共8个数。因为摸出2的整数倍和摸出不是2的整数倍的可能性是不一样的,即小明和小芳赢的可能性不相等,所以这个游戏规则不公平。
(2)小明赢的可能比较小,但是实际操作过程中存在偶然性,小明不一定会输。
(3)要想使游戏规则公平,只要让两人赢的可能性相等即可。

2. 甲、乙两人玩掷骰子游戏,一共有两个骰子,每个骰子6个面上的点数分别是1、2、3、4、5、6。游戏规则是任意一人掷骰子,两个点数相乘的积作为最后的结果,如果两个骰子的点数之积是单数,那么甲赢;如果两个骰子的点数之积是双数,那么乙赢。这个游戏规则公平吗?为什么?

答案： 2.不公平,因为两人的投掷情况共有6×6=36(种),点数之积是单数的有9种,点数之积是双数的有27种,所以游戏规则是不公平的。[提示]将两人的投掷情况进行列举,并用乘法计算,求出积之后,再看结果是单数还是双数,发现单数只有9种,而双数有27种,很明显双数出现的可能性要远大于单数出现的可能性,游戏规则不公平。

3. 一个口袋里有1个红球、1个白球和3个黄球,共5个球,从中任意摸出3个球,摸到的球是1个红球、1个白球和1个黄球的可能性大,还是1个白球和2个黄球的可能性大?为什么?

答案：
3.可能性相等,因为一共有10种结果,其中摸到1个红球、1个白球和1个黄球的有3种情况,摸到1个白球和2个黄球的也有3种情况。[提示]在解决本题时,要按一定的顺序,列举出摸出的3个球的所有可能情况,做到不重复、不遗漏,列举出所有可能发生的情况后,再进行判断。如下表: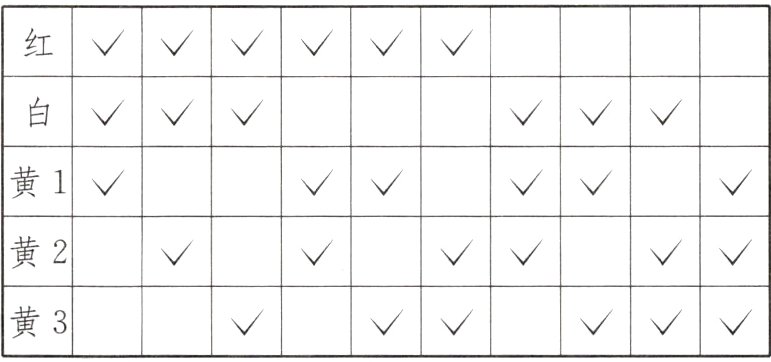一共有10种结果,因为摸到1红1白1黄的有3种情况,摸到1白2黄的也有3种情况,所以可能性相等。

4. 把4个红球、3个黄球、2个蓝球和1个白球四种颜色的球放入一个袋子里。任意摸一个球,摸到(红)球的可能性最大。若要保证摸到两个颜色相同的球,则至少需要取出(5)个球。

答案： 4.红 5 [提示]把4个红球、3个黄球、2个蓝球和1个白球四种颜色的球放入到一个袋子里。任意摸一个球,由于红球的个数最多,则摸到红球的可能性最大;袋子中一共有4种颜色的球,由抽屉原理可知,从中至少摸出4+1=5(个)球,才能保证摸到两个颜色相同的球。