《2025年实验班提优训练四年级数学上册苏教版》

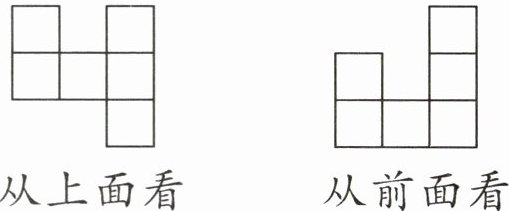
例 用小正方体搭一个立体图形,从上面和前面看到的图形如下图所示,搭这个立体图形最少要多少个小正方体？最多呢？
从上面看
从前面看

解析
观察从上面看到的图形,第一列有两行,结合从前面看到的图形,第一列中至少有一行有两层小正方体。同样,第二列只有一行,这一行只有一层小正方体；第三列有三行,其中至少有一行有三层小正方体。因此小正方体的个数最少为$(1+2)+1+(3+1+1)= 9$(个),最多为$(2+2)+1+(3+3+3)= 14$(个)。
答案：搭这个立体图形最少要9个小正方体,最多要14个小正方体。

答案： B

1. 用6个大小相同的正方体摆成一个长方体,从摆放的长方体的前面看,最多能看到多少种不同的形状？想一想,画一画。

答案：
以从前面看到的正方形的个数为分类依据，从前面看到的分别是1个正方形、2个正方形、3个正方形和6个正方形。
1个正方形
2个正方形
3个正方形
6个正方形

综上可知，从摆放的长方体的前面看，最多能看到9种不同的形状。
[提示]解决此类问题，可以先将可能的摆法进行分类，一般以某个固定方向观察到的图形包含的正方形的数量为分类依据，再考虑同样多数量的正方形不同的排列方式，注意做到不重复、不遗漏。

2. 左下图是一个由若干个同样的小正方体搭建而成的立体图形从前面和右面看到的形状,小刚用小正方体搭建以后,认为右下图中的三个形状都可以是该立体图形从上面看到的形状,你同意他的看法吗？并写出每个形状最少用了多少个小正方体？

答案：
我同意他的看法。①号图形最少用了11个小正方体；②号图形最少用了7个小正方体；③号图形最少用了7个小正方体。
[提示]①号摆成 时，用的小正方体最少，用了2+2+1×7=11(个)小正方体；②号摆成 时，用的小正方体最少，2+2+1×3=7(个)小正方体；③号摆成 时，用的小正方体最少，用了2+2+1×3=7(个)小正方体。

3. 一个立体图形从前面看到的形状是,从上面看到的形状是,从左面看到的形状是。搭一搭,用了( )个小正方体。

答案：
5 [提示]由从上面看到的形状可搭出的立体图形是，再由从前面看到的形状可搭出的立体图形是 ，与从左面看到的形状相比较，这个立体图形是