《2025年中学生世界六年级数学上册沪教版五四制》

23. (7 分)一个角的余角与这个角的补角的和为 130°,求这个角的度数.

答案： 设这个角的度数为 $x$。
根据余角和补角的定义：
这个角的余角为 $90^{\circ} - x$。
这个角的补角为 $180^{\circ} - x$。
根据题意，这个角的余角与补角的和为 $130^{\circ}$，可以列出方程：
$90^{\circ} - x + 180^{\circ} - x = 130^{\circ}$，
合并同类项，得到：
$270^{\circ} - 2x = 130^{\circ}$，
移项并化简，得到：
$-2x = -140^{\circ}$，
解得：
$x = 70^{\circ}$。
答：这个角的度数为 $70^{\circ}$。

24. (7 分)如图,已知 M,N 是线段 AB 上两点,且 AM=$\frac{2}{3}$MB,AN=4NB. 若 MN=6 cm,求线段 AB 的长.

答案： 设线段$ AB $的长为$ x $ cm。
1. 用$ AB $表示$ AM $和$ MB $：
因为$ AM = \frac{2}{3}MB $，且$ AM + MB = AB $，设$ MB = y $，则$ AM = \frac{2}{3}y $。
所以$ AB = \frac{2}{3}y + y = \frac{5}{3}y $，解得$ y = \frac{3}{5}AB $，即$ MB = \frac{3}{5}x $，$ AM = \frac{2}{3} × \frac{3}{5}x = \frac{2}{5}x $。
2. 用$ AB $表示$ AN $和$ NB $：
因为$ AN = 4NB $，且$ AN + NB = AB $，设$ NB = z $，则$ AN = 4z $。
所以$ AB = 4z + z = 5z $，解得$ z = \frac{1}{5}AB $，即$ NB = \frac{1}{5}x $，$ AN = 4 × \frac{1}{5}x = \frac{4}{5}x $。
3. 确定$ M $、$ N $位置并计算$ MN $：
由$ AM = \frac{2}{5}x $，$ AN = \frac{4}{5}x $，可知$ M $、$ N $在$ AB $上的顺序为$ A \to M \to N \to B $。
因此$ MN = AN - AM = \frac{4}{5}x - \frac{2}{5}x = \frac{2}{5}x $。
4. 求解$ AB $的长：
已知$ MN = 6 $ cm，即$ \frac{2}{5}x = 6 $，解得$ x = 6 × \frac{5}{2} = 15 $。
答：线段$ AB $的长为$ 15 $ cm。

25. (8 分)如图,已知∠AOB=110°,∠COD=70°,OA 平分∠EOC,OB 平分∠DOF,求∠EOF 的大小.

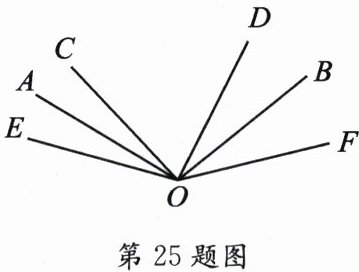
答案： 150°

26. (8 分)如图,在△ABC 中,点 O 是∠ABC 与∠ACB 的平分线的交点. 已知∠A=60°,求∠BOC 的度数.（提示:三角形的三个内角和为 180°）

答案：
∵在△ABC中，∠A=60°，三角形内角和为180°，
∴∠ABC + ∠ACB = 180° - ∠A = 180° - 60° = 120°。
∵BO、CO分别平分∠ABC、∠ACB，
∴∠OBC = 1/2∠ABC，∠OCB = 1/2∠ACB。
∴∠OBC + ∠OCB = 1/2(∠ABC + ∠ACB) = 1/2×120° = 60°。
在△BOC中，∠BOC = 180° - (∠OBC + ∠OCB) = 180° - 60° = 120°。
答：∠BOC的度数为120°。