《2025年中学生世界六年级数学上册沪教版五四制》

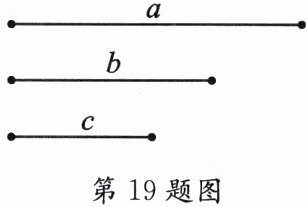
19. (5 分)如图,已知线段 a、b、c,用直尺和圆规求作一条线段,使它等于 a-b+c.（不写作法,保留作图痕迹,标明字母说明结论）

答案： 作图步骤：
1. 作射线 $ OP $；
2. 在射线 $ OP $ 上截取 $ OA = a $；
3. 以 $ A $ 为端点，在 $ OA $ 上截取 $ AB = b $，得 $ OB = a - b $；
4. 以 $ B $ 为端点，沿射线 $ OP $ 方向截取 $ BC = c $。
结论： 线段 $ OC $ 即为所求，$ OC = a - b + c $。
（注：保留作图痕迹，包括截取 $ a $、$ b $、$ c $ 时的圆弧交点及对应字母 $ O, A, B, C $。）

20. (5 分)如图,已知∠α和∠β,用直尺和圆规作图:（不写作法,保留作图痕迹,标明字母,说明结论）
(1)作一个∠ABC=∠α+∠β;
(2)在(1)的条件下,作∠ABC 的平分线 BD.

答案：
(1) 如图，∠ABC即为所求作的∠α+∠β。
(2) 如图，射线BD即为∠ABC的平分线。
（注：实际作答需在图中保留圆规画弧痕迹，标明点A、B、C、D及射线BA、BC、BD。）

21. (6 分)灯塔 A 在灯塔 B 的南偏东 30°方向,A、B 相距 4 海里,轮船 C 在灯塔 B 的正东方向、在灯塔 A 的北偏东 30°方向. 试画出轮船 C 的位置,并量出灯塔 A 和轮船 C 的距离（每海里画 1 cm）.

答案： 1. 确定灯塔B的位置。
2. 以B为顶点，作南偏东30°方向射线，截取BA=4cm（表示4海里），确定A点。
3. 过B点作正东方向射线（水平线向右）。
4. 以A为顶点，作北偏东30°方向射线，与B点正东方向射线交于点C。
5. 测量得AC=4cm，即AC=4海里。
灯塔A和轮船C的距离为4海里。

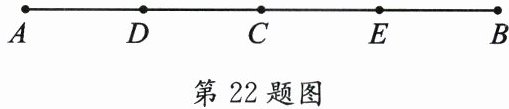
22. (6 分)如图,C 是线段 AB 的中点,D 是线段 AC 的中点,E 是线段 CB 的中点. 已知 BE=1.2 cm,求线段 AE,DE 的长度.

答案：
∵E是线段CB的中点，BE=1.2 cm，
∴CB=2BE=2×1.2=2.4 cm。
∵C是线段AB的中点，
∴AC=CB=2.4 cm，AB=2CB=4.8 cm。
∴AE=AB-BE=4.8-1.2=3.6 cm。
∵D是线段AC的中点，
∴DC=AC/2=2.4/2=1.2 cm。
∵E是线段CB的中点，
∴CE=EB=1.2 cm。
∴DE=DC+CE=1.2+1.2=2.4 cm。
AE=3.6 cm，DE=2.4 cm。