《2025年综合应用创新题典中点七年级数学上册人教版》

1. [2025郑州中原区期中]如果长方形的周长为6m,一边长为m-2n,则另一边长为( )

A.2m+2n
B.m+n
C.2m+3n
D.m+2n

答案： A

2. 式子$x^2y-4x^2y+4x^3+3(2x^3y+x^2y)-2(3x^3y+2x^3+3)$的值( )

A.只与x有关
B.只与y有关
C.与x,y有关
D.与x,y无关

答案： D

3. 情境题 生活应用 如图,设M,N分别为天平左、右盘中物体的质量,且$M= 2m^2+m+3,N= 2m^2+2m+3,$当m＞0时,天平( )

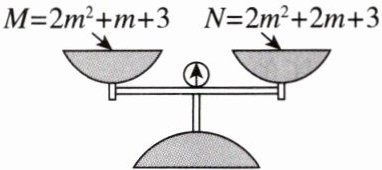
A.向左边倾斜
B.向右边倾斜
C.平衡
D.无法判断
]

答案： B 【点拨】$M-N=2m^{2}+m+3-(2m^{2}+2m+3)=2m^{2}+m+3-2m^{2}-2m-3=-m$. 因为$m＞0$,所以$-m＜0$. 所以$M＜N$. 所以天平向右边倾斜.

4. 情境题·生活应用 2025·武汉江汉区期中 某果园引入了m个采摘机器人,这些机器人被分为两组,每组的工作效率不同。第一组有n个机器人,每个机器人平均8秒采摘一个苹果；第二组包含剩余的机器人,每个机器人平均6秒采摘一个苹果。同时,果园内还有10名熟练的采摘工人,他们每个人平均5秒采摘一个苹果。机器人与工人同时工作1小时,则这m个机器人比这10名工人多采摘的苹果个数是( )

A.120(m-2n)-720
B.600m-150n-7200
C.600m+450n-7200
D.120m-150n-720

答案： B

5. 一名粗心的同学在计算$3a^2-a-4$加上一个多项式时,误看成减去这个多项式,得到$a^2+3,$那么正确的结果应该是_________。

答案： $5a^{2}-2a-11$ 【点拨】由题意,得这个多项式为$3a^{2}-a-4-(a^{2}+3)=3a^{2}-a-4-a^{2}-3=2a^{2}-a-7$,所以$3a^{2}-a-4+2a^{2}-a-7=5a^{2}-2a-11$.

6. 计算：
(1) $\frac{1}{2}x + 3(-2z + y) - (\frac{1}{3}x - 4y - 5z)$；
(2) $(4x^my^n - 8x^ny^m) - (-5x^ny^m - 3x^my^n)$；
(3) $2a^2b + 2ab^2 - 1 - [3(a^2b - 1) + ab^2 + 2]$。

答案： 【解】
(1)原式$=\frac{1}{2}x-6z+3y-\frac{1}{3}x+4y+5z=\frac{1}{6}x+7y-z$.
(2)原式$=4x^{m}y^{n}-8x^{n}y^{m}+5x^{n}y^{m}+3x^{m}y^{n}=7x^{m}y^{n}-3x^{n}y^{m}$.
(3)原式$=2a^{2}b+2ab^{2}-1-3a^{2}b+3-ab^{2}-2=-a^{2}b+ab^{2}$.

7. 母题 教材P102习题T4 先化简,再求值：
$3a^2b - [2ab^2 - 2(ab - \frac{3}{2}a^2b) + ab] + 3ab^2$,其中$a = 3$,$b = -\frac{1}{3}$。

答案： 【解】原式$=3a^{2}b-(2ab^{2}-2ab+3a^{2}b+ab)+3ab^{2}=3a^{2}b-2ab^{2}+2ab-3a^{2}b-ab+3ab^{2}=ab+ab^{2}$,
当$a=3,b=-\frac{1}{3}$时,
原式$=3×(-\frac{1}{3})+3×(-\frac{1}{3})^{2}=-1+3×\frac{1}{9}=-1+\frac{1}{3}=-\frac{2}{3}$.

8. 已知关于x的多项式$mx^2-mx-2$与$3x^2+mx+m$的和是单项式,则代数式$m^2-4m+4$的值是( )

A.25
B.0
C.2或-3
D.25或0

答案： D 【点拨】$mx^{2}-mx-2+3x^{2}+mx+m=(m+3)x^{2}+m-2$. 因为关于$x$的多项式$mx^{2}-mx-2$与$3x^{2}+mx+m$的和是单项式,所以$m+3=0$或$m-2=0$,所以$m=-3$或$m=2$. 当$m=-3$时,$m^{2}-4m+4=25$;当$m=2$时,$m^{2}-4m+4=0$. 综上,代数式$m^{2}-4m+4$的值是25或0.

9. 新考法 数形结合法 已知两个完全相同的大长方形,各放入四个完全一样的白色小长方形后,得到如图①,图②所示的图形,若要求出图①与图②中阴影部分周长的差,则下列说法错误的是( )

A.只需知道图①中EP的长
B.只需知道图①中EH的长
C.只需知道图①中FG的长
D.只需知道图①中GH的长
]

答案： D 【点拨】设题图中小长方形的宽为$x$,长为$y$,大长方形的宽为$b$,长为$a$,根据题意,得$2x+y=a,2x=y$,则$2y=a$,所以$EH=a-y=y$. 故易得题图①中阴影部分的周长为$2b+4y=2a+2b$,题图②中阴影部分的周长为$2(a+b-y)=2a+2b-2y$,所以题图①中阴影部分的周长与题图②中阴影部分周长的差为$(2a+2b)-(2a+2b-2y)=2y=a=4x$,即题图①与题图②中阴影部分周长的差为$4FG=EP=2EH$.