《2025年综合应用创新题典中点七年级数学上册人教版》

10. 正方形$ABCD$在数轴上的位置如图所示,点$D$,$A$对应的数分别为0和1.若正方形$ABCD绕着顶点A$按顺时针方向在数轴上连续翻转,翻转1次后,点$B$所对应的数为2,则翻转2024次后,数轴上数2025所对应的点是( )

A.点$A$
B.点$B$
C.点$C$
D.点$D$

答案： A

11. 如图,有一根木棒$MN$放置在单位长度为1cm的数轴上,它的两端$M$,$N分别落在点A$,$B$处.将木棒在数轴上水平移动,当点$M移动到点B$时,点$N$所表示的数为20,当点$N移动到点A$时,点$M$所表示的数为5,则木棒$MN$的长为______cm.

答案： 5

12. 长方形纸片上有一数轴,剪下8个单位长度(从$-2$到6)的一条线段,并把这条线段沿某点折叠,然后在重叠部分某处剪一刀得到三条线段.若这三条线段的长度之比为$1:1:2$,则折痕处对应的点所表示的数可能是______.

答案：
1或2或3 [点拨]因为三条线段的长度之比为1:1:2,所以设三条线段的长分别是x,x，2x.因为−2到6的距离是8,所以4x=8,解得x=2,所以三条线段的长分别为2,2,4.
　　如图①,当AB:BC:CD=1:1:2时,易知折痕处对应的点所表示的数是1;
　　　　
　　如图②,当AB:BC:CD=1:2:1时,易知折痕处对应的点所表示的数是2;
　　　　
　　如图③,当AB:BC:CD=2:1:1时,易知折痕处对应的点所表示的数是3.
　　　　
　　综上所述，折痕处对应的点所表示的数可能是1 或2或3.

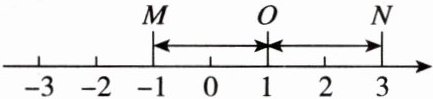
13. 在数轴上,表示数1的点记为$O$,我们把到点$O距离相等的两个不同点M和N$,称为基准1的对称点.例如：如图,点$M表示数-1$,点$N$表示数3,它们与表示数1的点$O$的距离都是2个单位长度,则点$M与点N$互为基准1的对称点.

(1)已知点$A表示数a$,点$B表示数b$,点$A与点B$互为基准1的对称点.
①若$a = 4$,则$b = $______；
②用含$a的式子表示b$,则$b = $______；
(2)对点$A$进行如下操作：先把点$A表示的数乘以\dfrac{5}{3}$,再把所得数对应的点沿着数轴向左移动2个单位长度得到点$B$.若点$A与点B$互为基准1的对称点,求点$A$表示的数.

答案： [解]
(1)①−2 ②2−a
(2)设点A表示的数为m，则点B表示的数为$\frac{5}{3}$m−2.
　因为点A与点B互为基准1的对称点，
　所以$\frac{5}{3}$m−2=2−m.
　所以$\frac{8}{3}$m=4,所以m=$\frac{3}{2}$.
　所以点A表示的数为$\frac{3}{2}$.

14. (1)借助数轴,回答下列问题：
①从$-1$到1有3个整数,分别是______；
②从$-2$到2有5个整数,分别是______；
③从$-100$到100有______个整数；
④从$-n$($n$为正整数)到$n$有______个整数.
(2)根据以上规律知,从$-3.9$到3.9有______个整数,从$-10.1$到10.1有______个整数.
(3)在单位长度是1cm的数轴上任意画一条长度为1000cm的线段$AB$,线段$AB$盖住的整数点最多有多少个？

答案：
[解]
(1)①−1,0,1 ②−2,−1,0,1,2
　　③201 ④(2n+1)
(2)7;21
(3)1000+1=1001(个),
[点拨]求较大范围内的整数点时，可类比较小范围内的情况.由图可知，1cm长的线段盖住的整数点的个数为1或2,2cm长的线段盖住的整数点的个数为2或3,故长为1000cm的线段盖住的整数点的个数为1000或1001.