《2025年综合应用创新题典中点七年级数学上册人教版》

1. 下列各式中,是代数式的有( )
① $3xy^{2}$；② $2\pi r$；③ $S = \pi r^{2}$；④ $b$；
⑤ $5 + 1 ＞ 2$；⑥ $\frac{ab}{2}$.

A.3 个
B.4 个
C.5 个
D.6 个

答案： 1.B 【点拨】由代数式的定义可知，是代数式的有：①$3xy^{2}$；②$2\pi r$；④$b$；⑥$\frac{ab}{2}$，共4个.

2. [2025 重庆綦江区期中] 下列代数式符合书写规范的是( )

A.$a5$
B.$\frac{xy}{5}$
C.$m + 2n$元
D.$-2\frac{3}{5}÷c$

答案： 2.B 【点拨】选项A正确的书写格式是$5a$，故此选项不符合题意；选项B正确，故此选项符合题意；选项C正确的书写格式是$(m+2n)$元，故此选项不符合题意；选项D正确的书写格式是$-\frac{13}{5c}$，故此选项不符合题意.

3. 下列关于代数式的意义不正确的是( )

A.$\frac{3a}{2}+4$表示 $a$ 的 3 倍与 4 的和的一半
B.$2(a + 5)$表示 $a$ 与 5 的和的 2 倍
C.$2a + 5$表示 $a$ 的 2 倍与 5 的和
D.$(a + b)^{2}$表示 $a$ 与 $b$ 的和的平方

答案： 3.A 【点拨】$\frac{3a+4}{2}$表示$a$的3倍与4的和的一半.

4. 一个两位数,十位数字是 $a$,十位数字比个位数字小 2,这个两位数是( )

A.$a(a + 2)$
B.$10a(a + 2)$
C.$10a + (a + 2)$
D.$10a + (a - 2)$

答案： 4.C

5. 如图,$A$,$B$ 两地之间有一条东西走向的道路.在 $A$ 地的东边 $5$ km 处设置第一个广告牌,之后每往东 $12$ km 就设置一个广告牌.一辆汽车从 $A$ 地的东边 $3$ km 处出发,沿此道路向东行驶.当经过第 $n$ 个广告牌时,此车所行驶的路程为( )


A.$(12n + 5)$km
B.$(12n + 2)$km
C.$(12n - 7)$km
D.$(12n - 10)$km

答案： 5.D 【点拨】由题意得当经过第$n$个广告牌时，此车所行驶的路程为$(5-3)+12(n-1)=(12n-10)(km)$.

6. 下面各组变量关系中,成正比例关系的是( )

A.人的身高与年龄
B.汽车从甲地到乙地,所用时间与行驶速度
C.正方形的面积与它的边长
D.圆的周长与它的半径

答案： 6.D

7. 母题 教材 P74 例 5 俊俊想存钱购买一套售价为 6 000 元的户外活动设备,若他目前已有存款 2 000 元,后期每个月计划存相同金额,用式子表示他存够买设备的钱所需月数 $y$ 与每个月存款额 $x$ 元之间的关系,$y$ 与 $x$ 成什么比例关系？

答案： 7.【解】根据题意，得$2000+xy=6000$，所以$xy=4000$或$y=\frac{4000}{x}$.所以$y$与$x$成反比例关系.

8. 若 $|x - 2|+(y + 6)^{2}= 0$,则 $2x - y$ 的值为( )

A.8
B.10
C.-8
D.-2

答案： 8.B 【点拨】因为$|x-2|+(y+6)^{2}=0$，所以$x-2=0$，$y+6=0$，所以$x=2$，$y=-6$，所以$2x-y=2×2-(-6)=4+6=10$.

9. [2025 成都锦江区月考] 已知 $a - 2b^{2}-3 = 0$,则 $2025 - 2a + 4b^{2}$ 的值是( )

A.2 019
B.2 022
C.2 028
D.2 031

答案： 9.A 【点拨】由$a-2b^{2}-3=0$，得$a-2b^{2}=3$，所以$2025-2a+4b^{2}=2025-2(a-2b^{2})=2025-2×3=2019$.

10. 已知有理数 $a$,$b$,$c$ 满足 $a + b + c = 0$ 且 $abc ＞ 0$.若 $x = \frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}+\frac{|abc|}{abc}$,$y = |b + c|-|a|+2$,则 $x - y^{4}$ 的值为______.

答案： 10.-16 【点拨】因为$a+b+c=0$，所以$b+c=-a$，所以$y=|b+c|-|a|+2=|-a|-|a|+2=|a|-|a|+2=2$.因为有理数$a$，$b$，$c$满足$a+b+c=0$且$abc＞0$，所以有理数$a$，$b$，$c$必有一个正数，两个负数，不妨设$a＞0$，$b＜0$，$c＜0$，所以$x=\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}+\frac{|abc|}{abc}=\frac{a}{a}+\frac{-b}{b}+\frac{-c}{c}+\frac{abc}{abc}=1-1-1+1=0$，所以$x-y^{4}=0-2^{4}=-16$.

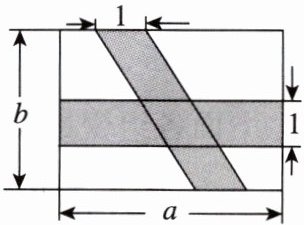
11. 如图是一个长为 $a$、宽为 $b$ 的长方形,两个阴影图形都是一对底边长为 1,且这对底边在长方形的对边上的平行四边形.
(1)用含字母 $a$,$b$ 的代数式表示长方形中空白部分的面积；
(2)当 $a = 3$,$b = 2$ 时,求长方形中空白部分的面积.

答案： 11.【解】
(1)由题意得长方形中空白部分的面积为$ab-1× a-1× b+1×1=ab-a-b+1$.
(2)当$a=3$，$b=2$时，$ab-a-b+1=3×2-3-2+1=2$.则长方形中空白部分的面积为2.