《2025年综合应用创新题典中点七年级数学上册人教版》

9. 绝对值大于$2.1而不大于6$的所有负整数的和是( )

A.$-12$
B.$-14$
C.$-18$
D.$-20$

答案： C 【点拨】绝对值大于2.1而不大于6的所有负整数有-3,-4,-5,-6,所以其和为(-3)+(-4)+(-5)+(-6)=-18.

10. 马小哈在计算一道有理数运算$\vert (-3)+\blacksquare\vert$时,一不小心将墨水泼在作业本上了,其中“$\blacksquare$”是被墨水污染看不清的一个数,他便问同桌,同桌故弄玄虚地说：“该题计算的结果等于$6$”,那么“$\blacksquare$”处的数是( )

A.$3$
B.$-3$
C.$3或-9$
D.$-3或9$

答案： D 【点拨】因为|(-3)+■|=6,所以(-3)+■=±6.所以■=-3或9.故选D.

11. 如图,在一条不完整的数轴上从左到右依次有三个点$A$,$B$,$C$,其中$AB = 2BC$,设点$A$,$B$,$C所对应的数的和为m$。若原点$O到点C的距离为6$,且$OC = AB$,则$m$的值为( )


A.$5或-20$
B.$6或-30$
C.$-20$
D.$-30$
]

答案：
B 【点拨】因为原点O到点C的距离为6,所以OC=6.分情况讨论:
①当点O位于点C左侧时,如图①,点C对应的数为6.
　　　　
因为OC=AB,AB=2BC,所以AB=6,BC=3.所以OB=OC-BC=6-3=3,即点B对应的数为3.所以OA=AB-OB=6-3=3,即点A对应的数为-3.所以m=(-3)+3+6=6;
②当点O位于点C右侧时,如图②,点C对应的数为-6.
　　　　
因为OC=AB,AB=2BC,所以AB=6,BC=3.所以OB=OC+BC=6+3=9,即点B对应的数为-9.所以OA=AB+OB=6+9=15,即点A对应的数为-15.所以m=(-15)+(-9)+(-6)=-30.
综上,m的值为6或-30.

12. 规定一种新运算“$*$”：$(+4)*(+16)= +20$,$(-10)*(-4)= +14$,$(-10)*(+14)= -24$,$(+15)* (-14)= -29$,$0*(-\frac{1}{2})= (-\frac{1}{2})*0= +\frac{1}{2}$,$0*(+1.4)= (+1.4)*0= +1.4$。根据“$*$”运算的法则,计算：$(-2.5)* [0*(-1\frac{3}{4})]= $______。

答案： -4.25 【点拨】$(-2.5)*\left[0*\left(-1\frac{3}{4}\right)\right]=(-2.5)*\left(+1\frac{3}{4}\right)=-\left(2.5+1\frac{3}{4}\right)=-4.25$.

13. 如图,从左到右,在每个小格子中都填入一个整数,使其中任意三个相邻格子中所填整数之和都相等,则$c= $______,第$2026$个格子中的数为______。
]

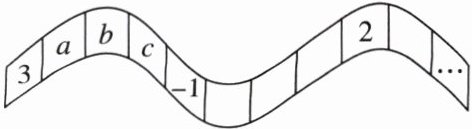
答案： 3;3 【点拨】因为任意三个相邻格子中所填整数之和都相等,所以3+a+b=a+b+c.所以c=3.因为a+b+c=b+c+(-1),所以a=-1.根据排列规律可得b=2,故这列数为3,-1,2,3,-1,2,…,3,-1,2,…因为2026÷3=675……1,所以第2026个格子中的数为3.

14. (1)用“$＞$”“$＜$”或“$=$”填空：
$\vert +5\vert+\vert +8\vert$______$\vert (+5)+(+8)\vert$；
$\vert -5\vert+\vert -8\vert$______$\vert (-5)+(-8)\vert$；
$\vert +5\vert+\vert -8\vert$______$\vert (+5)+(-8)\vert$；
$\vert -5\vert+\vert +8\vert$______$\vert (-5)+(+8)\vert$；
$0+\vert -8\vert$______$\vert 0+(-8)\vert$。
(2)根据(1)中的大小比较,猜想并归纳得出以下结论,请补充完整：
①当$a$,$b$______(填“同号”或“异号”)时,有$\vert a\vert+\vert b\vert＞\vert a + b\vert$；
②当$a$,$b$______(填“同号”或“异号”)时,有$\vert a\vert+\vert b\vert=\vert a + b\vert$；
③当$a$,$b中至少有一个为0$时,有$\vert a\vert+\vert b\vert$______$\vert a + b\vert$(填“$＞$”“$＜$”或“$=$”)。
④总之,对于有理数$a$,$b$,有$\vert a\vert+\vert b\vert$______$\vert a + b\vert$。
(3)根据以上结论,请直接写出当$\vert x\vert+2025= \vert x - 2025\vert$时,$x$的取值范围。

答案： 【解】
(1)=;=;＞;＞;=
(2)①异号 ②同号 ③= ④≥
(3)x的取值范围是x≤0.

15. 爱动脑筋的小明同学设计了一种“幻圆”游戏,将$1$,$-2$,$3$,$-4$,$5$,$-6$,$7$,$-8$分别填入图中的圆圈内,使横、竖以及内外两圈上的$4$个数字之和都相等,他已经将$-2$,$-6$,$7$,$-8$这四个数填入了圆圈,则图中$a + b$的值为______。
]

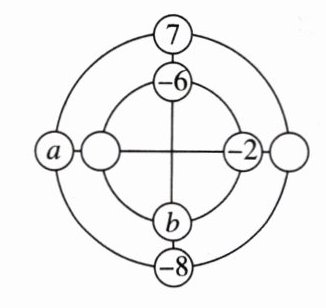
答案：
1或8 【点拨】设空白的两个圆圈内填入的数为x,y,如图,由题意,得b+x-6-2=7-6+b-8=a+x-2+y=a+7+y-8.所以x=1,b-6=a+y.所以a,b,y三个数应从3,-4,5中选,当a=3,b=5,y=-4时,b-6=a+y成立,此时,a+b=8;当a=3,b=-4,y=5时,b-6=a+y不成立;当a=-4,b=3,y=5时,b-6=a+y不成立;当a=-4,b=5,y=3时,b-6=a+y成立,此时,a+b=1;当a=5,b=3,y=-4时,b-6=a+y不成立;当a=5,b=-4,y=3时,b-6=a+y不成立.综上,a+b的值为1或8.