《2025年综合应用创新题典中点七年级数学上册人教版》

1. 下列各式化简后结果最大的是( )

A.$(-3)^{2}-(-2)^{3}$
B.$(-3 - 2)^{3}$
C.$(-3)^{3}×(-2^{2})$
D.$3^{3}+(-2)^{2}$

答案： C

2. 下列各式计算正确的是( )

A.$-3÷7×\frac{1}{7}= -3÷1= -3$
B.$-3^{2}-(-3)^{2}= -9 - 9= -18$
C.$(-1)^{4}×5+(-2)^{3}÷4= -7$
D.$3×2^{3}-2×9= 3×6 - 18= 0$

答案： B

3. 在算式$(-3)□(-4)^{2}·\left|-\frac{1}{5}\right|$中的“$□$”里填入下列运算符号,使得它的计算结果最小,则“$□$”里应填入的是( )

A.$+$
B.$-$
C.$×$
D.$÷$

答案： C

4. “24 点”游戏规则：从一副扑克牌抽去大小王剩下 1～13 这 52 张牌(A 代表 1),J,Q,K 分别代表 11,12,13,任意抽取 4 张牌称为牌组,黑色代表正数,红色代表负数,用加、减、乘、除、乘方把牌面上的数算成 24,每张牌必须用且只能用一次.如果抽到黑桃 Q、红桃 Q、梅花 3、方块 A,请列出一个含有乘方运算的算式,将该牌面上的数字凑成 24：______.

答案： 12+(-12)×(-1)³(答案不唯一)

5. 计算：
(1)$3^{2}×(\frac{1}{3}+\frac{1}{9})+(-2)^{3}$；
(2)$-1^{4}+2÷[8÷(-2)^{4}]-\left|-\frac{3}{2}\right|×(-1)^{2027}$；
(3)$\left[-2^{4}÷(-2\frac{2}{3})^{2}+5\frac{1}{2}×(-\frac{1}{6})-\frac{1}{4}\right]÷\frac{1}{12}$；
(4)$3×\left[5^{2}-6+(-8)^{2}-2×(-2)^{3}×\frac{1}{4}\right]÷(-3)^{3}$.

答案： 【解】
(1)原式=9×$\frac{4}{9}$-8=-4.
(2)原式=-1+2÷(8÷16)-$\frac{3}{2}$×(-1)=-1+2÷$\frac{1}{2}$+$\frac{3}{2}$=-1+4+$\frac{3}{2}$=$\frac{9}{2}$.
(3)原式=(-16×$\frac{9}{64}$-$\frac{11}{2}$×$\frac{1}{6}$-$\frac{1}{4}$)×12=(-$\frac{5}{2}$-$\frac{11}{12}$)×12=-$\frac{5}{2}$×12-$\frac{11}{12}$×12=-30-11=-41.
(4)原式=3×(25-6+64+2×8×$\frac{1}{4}$)×(-$\frac{1}{27}$)=3×(25-6+64+4)×(-$\frac{1}{27}$)=3×87×(-$\frac{1}{27}$)=-$\frac{29}{3}$.

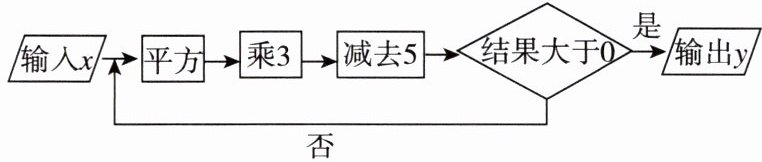
6. 根据如图的流程图计算,若输入 $x$ 的值为 0,则输出 $y$ 的值为( )


A.5
B.7
C.70
D.187

答案： C 【点拨】将x=0代入，结果为0²×3-5=-5＜0，将x=-5代入，结果为(-5)²×3-5=25×3-5=70＞0，所以输出y的值为70.

7. 若 $a$,$b$ 互为相反数,$c$,$d$ 互为倒数,且 $b≠0$,则$(a + b)^{2026}+(cd)^{2025}+(\frac{a}{b})^{2026}$的值为( )

A.3
B.2
C.1
D.0

答案： B

8. 已知 $a$,$b$,$c$,$d$ 都是负数,且$\left|x_{1}+a\right|+\left|x_{2}+b\right|+\left|x_{3}+c\right|+\left|x_{4}+d\right|=0$,则$\frac{x_{1}x_{2}}{x_{3}x_{4}}$的值为( )

A.负数
B.0
C.正数
D.负数或 0

答案： C 【点拨】因为|x₁+a|+|x₂+b|+|x₃+c|+|x₄+d|=0，所以|x₁+a|=|x₂+b|=|x₃+c|=|x₄+d|=0，所以x₁=-a，x₂=-b，x₃=-c，x₄=-d.因为a，b，c，d都是负数，所以$\frac{x₁x₂}{x₃x₄}$=$\frac{(-a)·(-b)}{(-c)·(-d)}$=$\frac{ab}{cd}$＞0，故选C.

9. 如图,在正五边形中,已知 $a$,$b$,$c$,$d$,$e$ 为正整数,且每条边上的三个数之和都等于$-3$,则 $c^{3}+a - b - d - e= $______.

答案： 117 【点拨】由题图和题意，可知a+b=-3-(-7)=4，b+c=-3-(-11)=8，a+e=-3-(-8)=5，c+d=-3-(-10)=7，d+e=-3-(-9)=6.因为a，b，c，d，e为正整数，所以0＜a＜4，且a为正整数，当a=1时，易知b=3，c=5，d=2，e=4，所以c³+a-b-d-e=5³+1-3-2-4=117；当a=2时，易知b=2，c=6，d=1，e=5.因为当e=5时，a=0，与a=2矛盾，所以不符合题意；当a=3时，易知b=1，c=7，d=0，不符合题意.故答案为117.