《2025年暑假乐园海南出版社五年级数学人教版》

四、下面各题,怎么简便就怎么算。
$\frac {7}{8}-(\frac {3}{8}+\frac {1}{9})$ $\frac {5}{8}+(\frac {5}{6}-\frac {1}{24})$ $1.6×2.5×1.25$

答案： 【解析】：
1. 计算$\frac{7}{8}-(\frac{3}{8}+\frac{1}{9})$：
根据去括号法则$a-(b + c)=a - b - c$，则$\frac{7}{8}-(\frac{3}{8}+\frac{1}{9})=\frac{7}{8}-\frac{3}{8}-\frac{1}{9}$。
先计算$\frac{7}{8}-\frac{3}{8}=\frac{7 - 3}{8}=\frac{4}{8}=\frac{1}{2}$，再计算$\frac{1}{2}-\frac{1}{9}=\frac{9}{18}-\frac{2}{18}=\frac{9 - 2}{18}=\frac{7}{18}$。
2. 计算$\frac{5}{8}+(\frac{5}{6}-\frac{1}{24})$：
先对括号内的分数进行通分，$\frac{5}{6}-\frac{1}{24}=\frac{20}{24}-\frac{1}{24}=\frac{20 - 1}{24}=\frac{19}{24}$。
再计算$\frac{5}{8}+\frac{19}{24}$，$\frac{5}{8}=\frac{15}{24}$，则$\frac{15}{24}+\frac{19}{24}=\frac{15 + 19}{24}=\frac{34}{24}=\frac{17}{12}$。
3. 计算$1.6×2.5×1.25$：
把$1.6$拆分为$0.2×8$，则原式变为$(0.2×2.5)×(8×1.25)$。
根据乘法结合律$(a×b)×c=a×(b×c)$，$0.2×2.5 = 0.5$，$8×1.25 = 10$，所以$0.5×10 = 5$。
【答案】：$\frac{7}{18}$；$\frac{17}{12}$；$5$

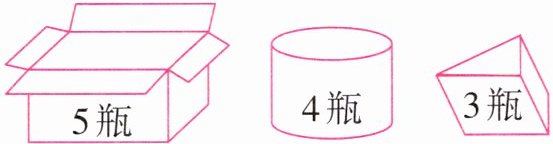
1. 如右图,哪种包装盒可以把70瓶饮料正好装完? 需要几个包装盒?

答案： 【解析】：
- 对于$5$瓶/盒的包装盒：$70\div5 = 14$（个），没有余数，说明$70$瓶饮料可以用$5$瓶/盒的包装盒正好装完。
- 对于$4$瓶/盒的包装盒：$70\div4 = 17\cdots\cdots2$，有余数，说明$70$瓶饮料不能用$4$瓶/盒的包装盒正好装完。
- 对于$3$瓶/盒的包装盒：$70\div3 = 23\cdots\cdots1$，有余数，说明$70$瓶饮料不能用$3$瓶/盒的包装盒正好装完。
【答案】：$5$瓶的包装盒可以把$70$瓶饮料正好装完，需要$14$个包装盒。

2. 一篮鸡蛋,2个2个地数,3个3个地数或5个5个地数,都正好数完,这篮鸡蛋至少有多少个?

答案： 【解析】：本题可根据最小公倍数的概念来求解这篮鸡蛋至少有多少个。
已知这篮鸡蛋$2$个$2$个地数，$3$个$3$个地数或$5$个$5$个地数都正好数完，说明鸡蛋的个数是$2$、$3$、$5$的公倍数。
因为$2$、$3$、$5$这三个数两两互质（即除了$1$以外没有其他的公因数），所以它们的最小公倍数就是这三个数的乘积。
根据上述分析可计算$2$、$3$、$5$的最小公倍数为：$2\times3\times5 = 30$，即这篮鸡蛋至少有$30$个。
【答案】：$30$

3. 有一个三位数,同时是2和3的倍数,而且这个数各位上的数字都是互不相同的质数。这个三位数最小是多少? 最大是多少?
我是这样想的:

答案： 【解析】：
1. 首先明确质数的概念：
质数是指在大于$1$的自然数中，除了$1$和它本身以外不再有其他因数的自然数。$10$以内的质数有$2$、$3$、$5$、$7$。
2. 然后根据$2$的倍数的特征：
个位上是$0$、$2$、$4$、$6$、$8$的数是$2$的倍数，所以这个三位数的个位只能是$2$。
3. 接着根据$3$的倍数的特征：
一个数各位上的数字之和是$3$的倍数，这个数就是$3$的倍数。
设这个三位数为$abc$（$c = 2$），$a$、$b$从$3$、$5$、$7$中选。
当求最小的三位数时：
百位选除$2$外最小的质数，先尝试百位$a = 3$，十位$b$从剩下的$5$、$7$中选。若$b = 5$，则各位数字之和为$3 + 5+2=10$，不是$3$的倍数；若$b = 7$，则各位数字之和为$3 + 7 + 2=12$，$12\div3 = 4$，是$3$的倍数，所以最小的三位数是$372$。
当求最大的三位数时：
百位选最大的质数$7$，十位从剩下的$3$、$5$中选。若$b = 5$，则各位数字之和为$7 + 5+2 = 14$，不是$3$的倍数；若$b = 3$，则各位数字之和为$7+3 + 2=12$，$12\div3 = 4$，是$3$的倍数，所以最大的三位数是$732$。
【答案】：最小是$372$，最大是$732$