3. 如图 2,在矩形 $ ABCD $ 中,$ AB = 1 $,$ BC = 2 $,点 $ P $ 从点 $ B $ 出发,沿 $ B \to C \to D $ 向终点 $ D $ 匀速运动,设点 $ P $ 走过的路程为 $ x $,$ \triangle ABP $ 的面积为 $ S $,能正确反映 $ S $ 与 $ x $ 之间函数关系的图象是(
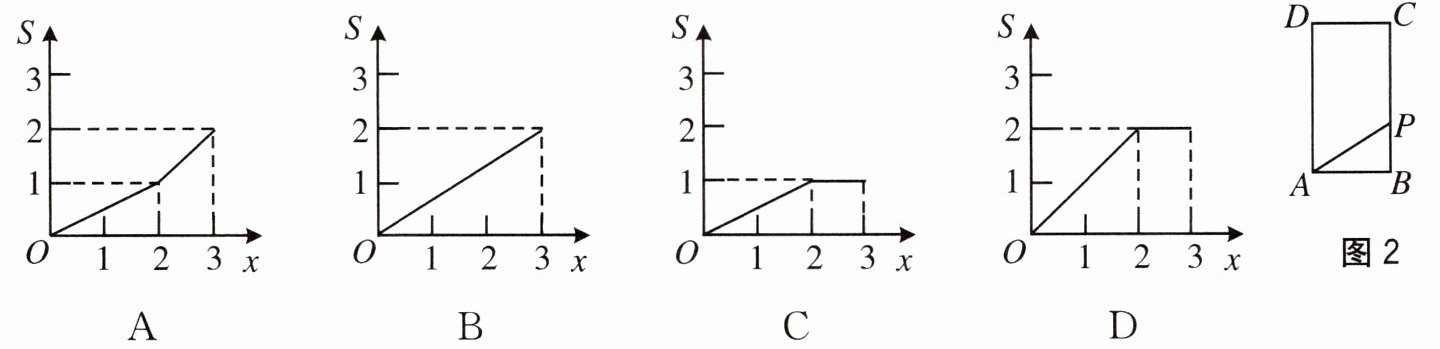
D
)。
答案:
$D$
4. 已知函数满足下列两个条件:①当 $ x > 0 $ 时,$ y $ 随 $ x $ 的增大而增大;②它的图象经过点 $ (1,-2) $。请写出一个符合上述条件的函数的表达式:
$y = 2x - 4$(答案不唯一)
。
答案:
$y = 2x - 4$(答案不唯一)
5. 若一次函数 $ y = (1 - k)x + 2k - 4 $ 的图象不过第一象限,则 $ k $ 的取值范围是
$1\lt k\leqslant2$
。
答案:
$1\lt k\leqslant2$
6. 数形结合是解决数学问题常用的思想方法。如图 3,直线 $ y = 2x - 1 $ 与直线 $ y = kx + b $($ k \neq 0 $)相交于点 $ P(2,3) $。根据图象可知,关于 $ x $ 的不等式 $ 2x - 1 > kx + b $ 的解集是(
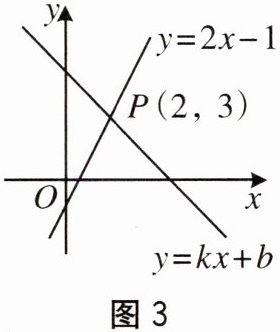
A. $ x < 2 $
B. $ x < 3 $
C. $ x > 2 $
D. $ x > 3 $
C
)。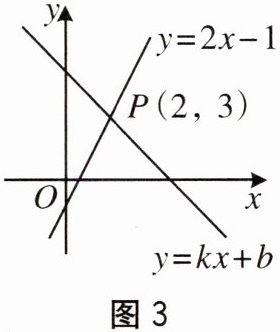
A. $ x < 2 $
B. $ x < 3 $
C. $ x > 2 $
D. $ x > 3 $
答案:
C
7. 如图 4 所示,在直角梯形 $ ABCD $ 中,$ AB // DC $,$ \angle B = 90^{\circ} $。动点 $ P $ 从点 $ B $ 出发,沿梯形的边由 $ B \to C \to D \to A $ 运动。设点 $ P $ 运动的路程为 $ x $,$ \triangle ABP $ 的面积为 $ y $。把 $ y $ 看作 $ x $ 的函数,函数的图象如图 5 所示,则 $ \triangle ACD $ 面积为(
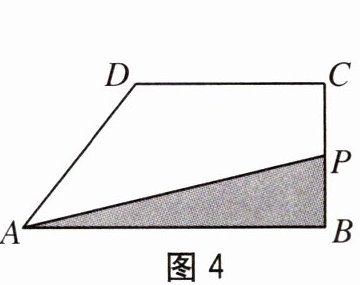
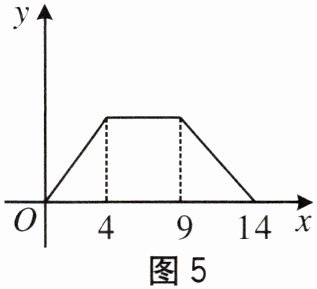
A. 10
B. 16
C. 18
D. 20
A
)。

A. 10
B. 16
C. 18
D. 20
答案:
A
查看更多完整答案,请扫码查看


