4. 要使一个矩形成为正方形,需添加的一个条件是
一组邻边相等(或对角线互相垂直)
.
答案:
一组邻边相等(或对角线互相垂直)
5. 如图2,正方形$ABCD$的周长为$16 cm$,顺次连接正方形$ABCD$各边的中点,得到四边形$EFGH$,则四边形$EFGH$的面积等于

8
$cm ^ { 2 }$.
答案:
$8$
6. 利用图形的分、和、移、补探索图形关系,是解决数学问题的一种重要方法. 如图3①,$BD$是矩形$ABCD$的对角线,将$\triangle BCD$分割成两对全等的直角三角形和一个正方形,然后按图3②重新摆放,观察两图,若$a = 4$,$b = 2$,则矩形$ABCD$的面积是

15
.
答案:
$15$
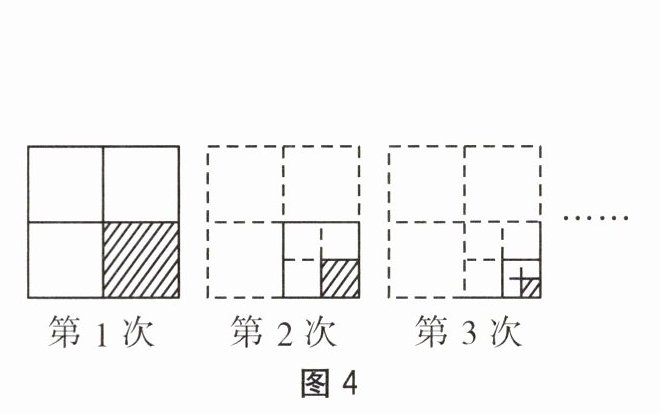
7. 如图4,将一张正方形纸片分割成四张面积相等的小正方形纸片,然后将其中一张小正方形纸片再分割成四张面积相等的小正方形纸片,如此分割下去. 第6次分割后,共有正方形纸片
19
张.
答案:
$19$
8. 如图5,点$A$在线段$BG$上,四边形$ABCD$和$DEFG$都是正方形,面积分别为16和20,求$\triangle CDE$的面积.


8
答案:
【解析】:
- 因为四边形$ABCD$是正方形,面积为$16$,根据正方形面积公式$S = a^{2}$($a$为边长),可得$CD^{2}=16$,则$CD = 4$。
- 因为四边形$DEFG$是正方形,面积为$20$,同理可得$DE^{2}=20$。
- 又因为$\angle ADC=\angle EDG = 90^{\circ}$,所以$\angle CDE+\angle ADG = 180^{\circ}$。
- 过点$E$作$EH\perp CD$交$CD$的延长线于$H$,则$\angle EHD = 90^{\circ}$。
- 因为$\angle DAG+\angle ADG = 180^{\circ}$,所以$\angle CDE=\angle DAG$。
- 又因为$\angle EHD=\angle DAG = 90^{\circ}$,$DE = DG$,所以$\triangle EDH\cong\triangle DGA$($AAS$),则$EH = DA$。
- 而$DA = CD = 4$(正方形$ABCD$的边长)。
- 根据三角形面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高),对于$\triangle CDE$,底$CD = 4$,高$EH = 4$,则$S_{\triangle CDE}=\frac{1}{2}\times CD\times EH$。
- 把$CD = 4$,$EH = 4$代入可得$S_{\triangle CDE}=\frac{1}{2}\times4\times4 = 8$。
【答案】:$8$
- 因为四边形$ABCD$是正方形,面积为$16$,根据正方形面积公式$S = a^{2}$($a$为边长),可得$CD^{2}=16$,则$CD = 4$。
- 因为四边形$DEFG$是正方形,面积为$20$,同理可得$DE^{2}=20$。
- 又因为$\angle ADC=\angle EDG = 90^{\circ}$,所以$\angle CDE+\angle ADG = 180^{\circ}$。
- 过点$E$作$EH\perp CD$交$CD$的延长线于$H$,则$\angle EHD = 90^{\circ}$。
- 因为$\angle DAG+\angle ADG = 180^{\circ}$,所以$\angle CDE=\angle DAG$。
- 又因为$\angle EHD=\angle DAG = 90^{\circ}$,$DE = DG$,所以$\triangle EDH\cong\triangle DGA$($AAS$),则$EH = DA$。
- 而$DA = CD = 4$(正方形$ABCD$的边长)。
- 根据三角形面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高),对于$\triangle CDE$,底$CD = 4$,高$EH = 4$,则$S_{\triangle CDE}=\frac{1}{2}\times CD\times EH$。
- 把$CD = 4$,$EH = 4$代入可得$S_{\triangle CDE}=\frac{1}{2}\times4\times4 = 8$。
【答案】:$8$
查看更多完整答案,请扫码查看


