11. 【教材呈现】
下面是人教版八年级下册数学教材18.1.1平行四边形的性质中的部分内容.
|探究:如图9,在$□ ABCD$中,连接$AC$,$BD$,并设它们相交于点$O$,$OA$与$OC$,$OB$与$OD$有什么关系?| |
|
|--|--|
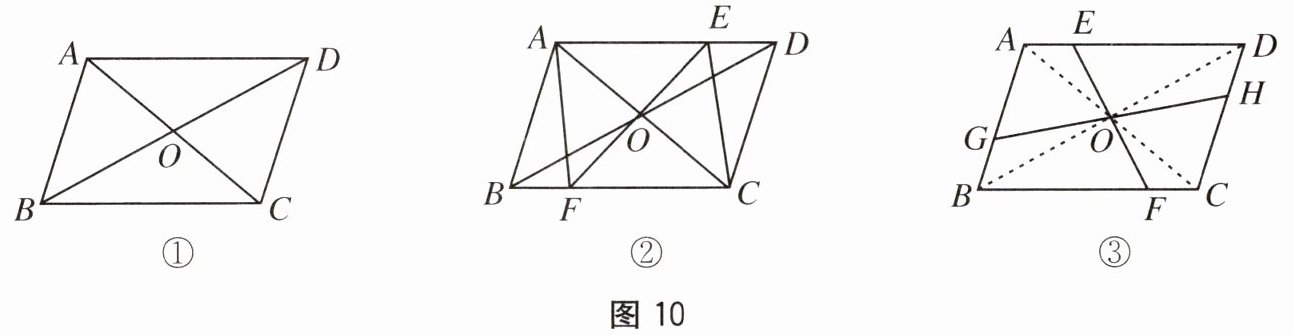
(1)如图10①,在$□ ABCD$中,$OA$与$OC$数量关系为
【性质应用】
(2)如图10②,$□ ABCD$的对角线$AC$,$BD$相交于点$O$,$EF$过点$O$且与$AD$,$BC$分别相交于点$E$,$F$. 连接$AF$,$CE$.
①求证:四边形$AECF$是平行四边形.
②若$EF\perp AC$,$\triangle ABF$周长是18,则$□ ABCD$的周长是
【拓展应用】
(3)如图10③,若四边形$ABCD$是平行四边形,过点$O$作直线$EF$分别交边$AD$,$BC$于点$E$,$F$,过点$O$作直线$GH$分别交边$AB$,$CD$于点$G$,$H$,且$S_{\text{四边形}AGOE}=\frac{1}{4}S_{□ ABCD}$. 若$AD=5$,$AB=3$,$BG=1$,则$AE=$
下面是人教版八年级下册数学教材18.1.1平行四边形的性质中的部分内容.
|探究:如图9,在$□ ABCD$中,连接$AC$,$BD$,并设它们相交于点$O$,$OA$与$OC$,$OB$与$OD$有什么关系?|
 |
||--|--|
(1)如图10①,在$□ ABCD$中,$OA$与$OC$数量关系为
$OA=OC$
,$OB$与$OD$数量关系为$OB=OD$
.(直接写出结果)【性质应用】
(2)如图10②,$□ ABCD$的对角线$AC$,$BD$相交于点$O$,$EF$过点$O$且与$AD$,$BC$分别相交于点$E$,$F$. 连接$AF$,$CE$.
①求证:四边形$AECF$是平行四边形.
②若$EF\perp AC$,$\triangle ABF$周长是18,则$□ ABCD$的周长是
36
.【拓展应用】
(3)如图10③,若四边形$ABCD$是平行四边形,过点$O$作直线$EF$分别交边$AD$,$BC$于点$E$,$F$,过点$O$作直线$GH$分别交边$AB$,$CD$于点$G$,$H$,且$S_{\text{四边形}AGOE}=\frac{1}{4}S_{□ ABCD}$. 若$AD=5$,$AB=3$,$BG=1$,则$AE=$
1
.
答案:
【解析】:
- (1)根据平行四边形的性质:平行四边形的对角线互相平分,可得$OA = OC$,$OB = OD$。
- (2)①证明:因为四边形$ABCD$是平行四边形,所以$AD// BC$,$OA = OC$,则$\angle OAE=\angle OCF$。
在$\triangle AOE$和$\triangle COF$中,$\begin{cases}\angle OAE=\angle OCF\\OA = OC\\\angle AOE=\angle COF\end{cases}$(对顶角相等),所以$\triangle AOE\cong\triangle COF(ASA)$,则$OE = OF$。
又因为$OA = OC$,根据“对角线互相平分的四边形是平行四边形”,所以四边形$AECF$是平行四边形。
②因为$EF\perp AC$,$OA = OC$,所以$EF$是$AC$的垂直平分线,则$AE = CE$。
$\triangle ABF$的周长$=AB + BF + AF=AB + BF + CE=AB + BC = 18$。
平行四边形$ABCD$的周长$=2(AB + BC)=2\times18 = 36$。
- (3)因为四边形$ABCD$是平行四边形,所以$S_{\triangle AOB}=\frac{1}{4}S_{\square ABCD}$。
已知$S_{\text{四边形}AGOE}=\frac{1}{4}S_{\square ABCD}$,所以$S_{\triangle AOB}=S_{\text{四边形}AGOE}$,即$S_{\triangle AOG}+S_{\triangle BOE}=S_{\triangle AOG}+S_{\triangle AOE}$,所以$S_{\triangle BOE}=S_{\triangle AOE}$。
因为$AB = 3$,$BG = 1$,所以$AG=AB - BG=3 - 1 = 2$。
过点$E$作$EM\perp AB$于点$M$,过点$O$作$ON\perp AB$于点$N$。
因为$O$是$AC$,$BD$中点,所以$ON$是$\triangle ABC$的中位线,$ON=\frac{1}{2}AD$($AD$为平行四边形的边,这里$AD$与$BC$平行且相等,$ON$与$AD$的关系可通过中位线性质推导)。
$S_{\triangle AOE}=\frac{1}{2}AG\cdot EM$,$S_{\triangle BOE}=\frac{1}{2}BG\cdot EM$(同高$EM$),因为$S_{\triangle BOE}=S_{\triangle AOE}$,所以$AG = BG$不成立,我们换一种思路。
因为四边形$ABCD$是平行四边形,$O$是对角线交点,所以$\triangle AOE\cong\triangle COF$,$\triangle AOG\cong\triangle COH$,$\triangle BOF\cong\triangle DOE$,$\triangle BOG\cong\triangle DOH$。
$S_{\text{四边形}AGOE}=\frac{1}{4}S_{\square ABCD}$,则$S_{\triangle AOG}+S_{\triangle AOE}=\frac{1}{4}S_{\square ABCD}$。
因为$S_{\triangle AOB}=\frac{1}{4}S_{\square ABCD}$,所以$S_{\triangle AOG}+S_{\triangle BOE}=S_{\triangle AOG}+S_{\triangle AOE}$,即$S_{\triangle BOE}=S_{\triangle AOE}$。
又因为$\triangle AOE$和$\triangle BOE$的高相同(以$AB$为底,过$E$作$AB$的垂线为高),所以$AG = BG$不成立,利用面积关系$S_{\text{四边形}AGOE}=\frac{1}{4}S_{\square ABCD}$,$S_{\square ABCD}=AB\times h$($h$为$AB$边上的高),$S_{\text{四边形}AGOE}=S_{\triangle AOG}+S_{\triangle AOE}$。
因为$O$是$BD$中点,$\triangle AOG$和$\triangle BOG$等底等高,$S_{\triangle AOG}=S_{\triangle BOG}$,同理$S_{\triangle AOE}=S_{\triangle DOE}$。
设$AE=x$,则$DE = 5 - x$。
$S_{\text{四边形}AGOE}=S_{\triangle AOG}+S_{\triangle AOE}$,$S_{\triangle AOG}=\frac{1}{2}AG\times\frac{1}{2}h$($h$为平行四边形$AB$边上的高,$O$到$AB$距离是$\frac{1}{2}h$),$S_{\triangle AOE}=\frac{1}{2}AE\times\frac{1}{2}h$。
$S_{\square ABCD}=AB\times h = 3h$,$S_{\text{四边形}AGOE}=\frac{1}{4}\times3h$。
$AG = 2$,则$\frac{1}{2}\times2\times\frac{1}{2}h+\frac{1}{2}x\times\frac{1}{2}h=\frac{1}{4}\times3h$,两边同时除以$\frac{1}{2}h$得$2 + x = 3$,解得$x = 1$,即$AE = 1$。
【答案】:
(1)$OA = OC$;$OB = OD$
(2)①证明过程如上述解析;②$36$
(3)$1$
- (1)根据平行四边形的性质:平行四边形的对角线互相平分,可得$OA = OC$,$OB = OD$。
- (2)①证明:因为四边形$ABCD$是平行四边形,所以$AD// BC$,$OA = OC$,则$\angle OAE=\angle OCF$。
在$\triangle AOE$和$\triangle COF$中,$\begin{cases}\angle OAE=\angle OCF\\OA = OC\\\angle AOE=\angle COF\end{cases}$(对顶角相等),所以$\triangle AOE\cong\triangle COF(ASA)$,则$OE = OF$。
又因为$OA = OC$,根据“对角线互相平分的四边形是平行四边形”,所以四边形$AECF$是平行四边形。
②因为$EF\perp AC$,$OA = OC$,所以$EF$是$AC$的垂直平分线,则$AE = CE$。
$\triangle ABF$的周长$=AB + BF + AF=AB + BF + CE=AB + BC = 18$。
平行四边形$ABCD$的周长$=2(AB + BC)=2\times18 = 36$。
- (3)因为四边形$ABCD$是平行四边形,所以$S_{\triangle AOB}=\frac{1}{4}S_{\square ABCD}$。
已知$S_{\text{四边形}AGOE}=\frac{1}{4}S_{\square ABCD}$,所以$S_{\triangle AOB}=S_{\text{四边形}AGOE}$,即$S_{\triangle AOG}+S_{\triangle BOE}=S_{\triangle AOG}+S_{\triangle AOE}$,所以$S_{\triangle BOE}=S_{\triangle AOE}$。
因为$AB = 3$,$BG = 1$,所以$AG=AB - BG=3 - 1 = 2$。
过点$E$作$EM\perp AB$于点$M$,过点$O$作$ON\perp AB$于点$N$。
因为$O$是$AC$,$BD$中点,所以$ON$是$\triangle ABC$的中位线,$ON=\frac{1}{2}AD$($AD$为平行四边形的边,这里$AD$与$BC$平行且相等,$ON$与$AD$的关系可通过中位线性质推导)。
$S_{\triangle AOE}=\frac{1}{2}AG\cdot EM$,$S_{\triangle BOE}=\frac{1}{2}BG\cdot EM$(同高$EM$),因为$S_{\triangle BOE}=S_{\triangle AOE}$,所以$AG = BG$不成立,我们换一种思路。
因为四边形$ABCD$是平行四边形,$O$是对角线交点,所以$\triangle AOE\cong\triangle COF$,$\triangle AOG\cong\triangle COH$,$\triangle BOF\cong\triangle DOE$,$\triangle BOG\cong\triangle DOH$。
$S_{\text{四边形}AGOE}=\frac{1}{4}S_{\square ABCD}$,则$S_{\triangle AOG}+S_{\triangle AOE}=\frac{1}{4}S_{\square ABCD}$。
因为$S_{\triangle AOB}=\frac{1}{4}S_{\square ABCD}$,所以$S_{\triangle AOG}+S_{\triangle BOE}=S_{\triangle AOG}+S_{\triangle AOE}$,即$S_{\triangle BOE}=S_{\triangle AOE}$。
又因为$\triangle AOE$和$\triangle BOE$的高相同(以$AB$为底,过$E$作$AB$的垂线为高),所以$AG = BG$不成立,利用面积关系$S_{\text{四边形}AGOE}=\frac{1}{4}S_{\square ABCD}$,$S_{\square ABCD}=AB\times h$($h$为$AB$边上的高),$S_{\text{四边形}AGOE}=S_{\triangle AOG}+S_{\triangle AOE}$。
因为$O$是$BD$中点,$\triangle AOG$和$\triangle BOG$等底等高,$S_{\triangle AOG}=S_{\triangle BOG}$,同理$S_{\triangle AOE}=S_{\triangle DOE}$。
设$AE=x$,则$DE = 5 - x$。
$S_{\text{四边形}AGOE}=S_{\triangle AOG}+S_{\triangle AOE}$,$S_{\triangle AOG}=\frac{1}{2}AG\times\frac{1}{2}h$($h$为平行四边形$AB$边上的高,$O$到$AB$距离是$\frac{1}{2}h$),$S_{\triangle AOE}=\frac{1}{2}AE\times\frac{1}{2}h$。
$S_{\square ABCD}=AB\times h = 3h$,$S_{\text{四边形}AGOE}=\frac{1}{4}\times3h$。
$AG = 2$,则$\frac{1}{2}\times2\times\frac{1}{2}h+\frac{1}{2}x\times\frac{1}{2}h=\frac{1}{4}\times3h$,两边同时除以$\frac{1}{2}h$得$2 + x = 3$,解得$x = 1$,即$AE = 1$。
【答案】:
(1)$OA = OC$;$OB = OD$
(2)①证明过程如上述解析;②$36$
(3)$1$
查看更多完整答案,请扫码查看


