1. 将菱形和矩形的对角线性质相比较,所具有的共同点是(
A. 对角线相等
B. 对角线互相平分
C. 对角线互相垂直
D. 每条对角线平分一组对角
B
).A. 对角线相等
B. 对角线互相平分
C. 对角线互相垂直
D. 每条对角线平分一组对角
答案:
1. B
2. 如图1,菱形的周长为4,一个内角为$60^{\circ}$,则较短的对角线长为(
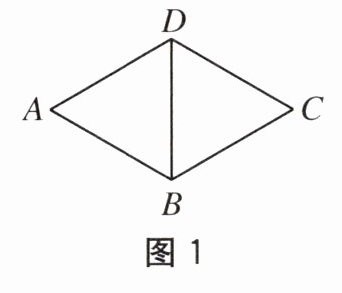
A. 2
B. $\sqrt{3}$
C. 1
D. $\dfrac{1}{2}$
C
).
A. 2
B. $\sqrt{3}$
C. 1
D. $\dfrac{1}{2}$
答案:
C
3. 将矩形纸片$ABCD$按如图2所示的方式折叠,得到菱形$AECF$. 若$AB=3$,则$BC$的长为(
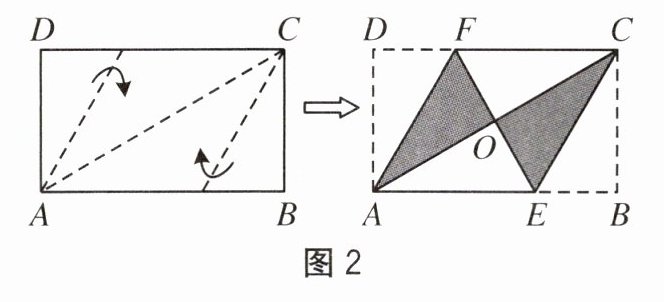
A. 1
B. 2
C. $\sqrt{2}$
D. $\sqrt{3}$
D
).
A. 1
B. 2
C. $\sqrt{2}$
D. $\sqrt{3}$
答案:
D
4. 如图3,在平面直角坐标系中,菱形$ABCD$对角线的交点坐标是$O(0,0)$,点$B$的坐标是$(0,1)$,且$BC=\sqrt{5}$,则点$A$的坐标是
$(-2,0)$
.
答案:
$(-2,0)$
查看更多完整答案,请扫码查看


