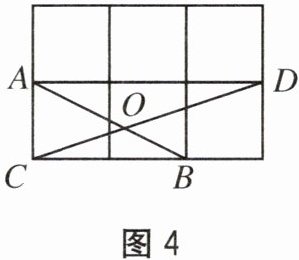
5. 如图 4 所示的是 $ 3×2 $ 的正方形网格,每个小正方形的顶点称为格点. 线段 $ AB $,$ CD $ 的端点均在格点上,线段 $ AB $,$ CD $ 交于点 $ O $,则 $ ∠BOD $ 的度数为(
A. $ 30^{\circ} $
B. $ 45^{\circ} $
C. $ 50^{\circ} $
D. $ 60^{\circ} $
B
).
A. $ 30^{\circ} $
B. $ 45^{\circ} $
C. $ 50^{\circ} $
D. $ 60^{\circ} $
答案:
B
6. 阅读理解:如果一个正整数 $ m $ 能表示为两个正整数 $ a $,$ b $ 的平方和,即 $ m = a^{2}+b^{2} $,那么称 $ m $ 为广义勾股数. 有下面的四个结论:①7 不是广义勾股数;②13 是广义勾股数;③两个广义勾股数的和是广义勾股数;④两个广义勾股数的积是广义勾股数. 其中正确的是(
A. ②④
B. ①②④
C. ①②
D. ①④
B
).A. ②④
B. ①②④
C. ①②
D. ①④
答案:
B
7. 学校在校园一角开辟了一块四边形的试验田 $ ABCD $(如图 5),学生们在课堂上学习理论之余,还可以到试验田实际操练,对生物的发展规律有更为直观的认识. 测得 $ AB = 9m $,$ BC = 12m $,$ CD = 8m $,$ AD = 17m $,且 $ ∠ABC = 90^{\circ} $,求这块四边形试验田的面积.


$114m^{2}$
答案:
【解析】:连接$AC$。
因为$\angle ABC = 90^{\circ}$,$AB = 9m$,$BC = 12m$,根据勾股定理$AC^{2}=AB^{2}+BC^{2}$,可得$AC=\sqrt{9^{2}+12^{2}}=\sqrt{81 + 144}=\sqrt{225}=15m$。
在$\triangle ACD$中,$AC = 15m$,$CD = 8m$,$AD = 17m$,因为$AC^{2}+CD^{2}=15^{2}+8^{2}=225 + 64 = 289$,$AD^{2}=17^{2}=289$,所以$AC^{2}+CD^{2}=AD^{2}$,根据勾股定理逆定理可知$\angle ACD = 90^{\circ}$。
那么四边形$ABCD$的面积$S = S_{\triangle ABC}+S_{\triangle ACD}$。
$S_{\triangle ABC}=\frac{1}{2}\times AB\times BC=\frac{1}{2}\times9\times12 = 54m^{2}$,$S_{\triangle ACD}=\frac{1}{2}\times AC\times CD=\frac{1}{2}\times15\times8 = 60m^{2}$。
所以$S = 54 + 60=114m^{2}$。
【答案】:$114m^{2}$
因为$\angle ABC = 90^{\circ}$,$AB = 9m$,$BC = 12m$,根据勾股定理$AC^{2}=AB^{2}+BC^{2}$,可得$AC=\sqrt{9^{2}+12^{2}}=\sqrt{81 + 144}=\sqrt{225}=15m$。
在$\triangle ACD$中,$AC = 15m$,$CD = 8m$,$AD = 17m$,因为$AC^{2}+CD^{2}=15^{2}+8^{2}=225 + 64 = 289$,$AD^{2}=17^{2}=289$,所以$AC^{2}+CD^{2}=AD^{2}$,根据勾股定理逆定理可知$\angle ACD = 90^{\circ}$。
那么四边形$ABCD$的面积$S = S_{\triangle ABC}+S_{\triangle ACD}$。
$S_{\triangle ABC}=\frac{1}{2}\times AB\times BC=\frac{1}{2}\times9\times12 = 54m^{2}$,$S_{\triangle ACD}=\frac{1}{2}\times AC\times CD=\frac{1}{2}\times15\times8 = 60m^{2}$。
所以$S = 54 + 60=114m^{2}$。
【答案】:$114m^{2}$
查看更多完整答案,请扫码查看


