6. 如果一个平行四边形的周长为80cm,且相邻两边之比为$1:3$,则长边=
30
cm,短边=10
cm.
答案:
30,10
7. 如图5,$□ ABCD$的对角线相交于点$O$,过点$O$任引直线交$AD$于点$E$,交$BC$于点$F$,则$OE$
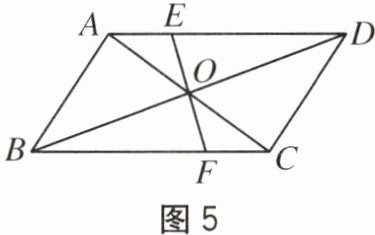
$=$
$OF$.(填“$>$”“$<$”或“$=$”)
答案:
$=$
8. 如图6,在$□ ABCD$中,过$AC$中点$O$作直线,分别交$AD$,$BC$于点$E$,$F$. 求证:$\triangle AOE\cong \triangle COF$.
证明:在$□ ABCD$中,$AD// BC$,$\therefore\angle EAO=\angle FCO$。$\because O$是$AC$中点,$\therefore AO = CO$。又$\because\angle AOE=\angle COF$,$\therefore\triangle AOE\cong\triangle COF$
证明:在$□ ABCD$中,$AD// BC$,$\therefore\angle EAO=\angle FCO$。$\because O$是$AC$中点,$\therefore AO = CO$。又$\because\angle AOE=\angle COF$,$\therefore\triangle AOE\cong\triangle COF$
$ASA$
。
答案:
【解析】:
- 因为四边形$ABCD$是平行四边形,根据平行四边形的性质,$AD// BC$。
- 由$AD// BC$,根据两直线平行,内错角相等,可得$\angle EAO=\angle FCO$。
- 已知$O$是$AC$的中点,所以$AO = CO$。
- 又因为对顶角相等,所以$\angle AOE=\angle COF$。
- 在$\triangle AOE$和$\triangle COF$中,$\left\{\begin{array}{l}\angle EAO=\angle FCO\\AO = CO\\\angle AOE=\angle COF\end{array}\right.$,根据角 - 边 - 角($ASA$)全等判定定理,可证$\triangle AOE\cong\triangle COF$。
【答案】:在$\square ABCD$中,$AD// BC$,$\therefore\angle EAO=\angle FCO$。$\because O$是$AC$中点,$\therefore AO = CO$。又$\because\angle AOE=\angle COF$,$\therefore\triangle AOE\cong\triangle COF(ASA)$。
- 因为四边形$ABCD$是平行四边形,根据平行四边形的性质,$AD// BC$。
- 由$AD// BC$,根据两直线平行,内错角相等,可得$\angle EAO=\angle FCO$。
- 已知$O$是$AC$的中点,所以$AO = CO$。
- 又因为对顶角相等,所以$\angle AOE=\angle COF$。
- 在$\triangle AOE$和$\triangle COF$中,$\left\{\begin{array}{l}\angle EAO=\angle FCO\\AO = CO\\\angle AOE=\angle COF\end{array}\right.$,根据角 - 边 - 角($ASA$)全等判定定理,可证$\triangle AOE\cong\triangle COF$。
【答案】:在$\square ABCD$中,$AD// BC$,$\therefore\angle EAO=\angle FCO$。$\because O$是$AC$中点,$\therefore AO = CO$。又$\because\angle AOE=\angle COF$,$\therefore\triangle AOE\cong\triangle COF(ASA)$。
9. 将两个大小不同的含$30^{\circ}$角的直角三角板按如图7所示的方式(无缝隙且不重叠)摆放在$□ ABCD$中,则$\angle 1$的度数为(
A. $50^{\circ}$
B. $60^{\circ}$
C. $75^{\circ}$
D. $80^{\circ}$
C
).A. $50^{\circ}$
B. $60^{\circ}$
C. $75^{\circ}$
D. $80^{\circ}$
答案:
C
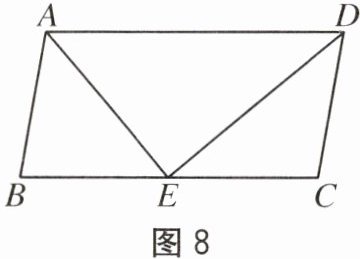
10. 如图8,已知在$□ ABCD$中,$DE$是$\angle ADC$的角平分线,交$BC$于点$E$.
(1)求证:$CD=CE$.
(2)若$BE=CE$,$\angle B=80^{\circ}$,求$\angle DAE$的度数.
(1)求证:$CD=CE$.
(2)若$BE=CE$,$\angle B=80^{\circ}$,求$\angle DAE$的度数.
50°

答案:
【解析】:
(1)因为四边形$ABCD$是平行四边形,所以$AD// BC$,根据两直线平行,内错角相等,可得$\angle ADE=\angle DEC$。
又因为$DE$是$\angle ADC$的角平分线,所以$\angle ADE=\angle CDE$。
从而$\angle DEC=\angle CDE$,根据等角对等边,可得$CD = CE$。
(2)因为四边形$ABCD$是平行四边形,所以$AB = CD$,$AD// BC$。
由(1)知$CD = CE$,又因为$BE = CE$,所以$AB = BE$。
因为$\angle B = 80^{\circ}$,在$\triangle ABE$中,根据等腰三角形两底角相等,可得$\angle BAE=\angle BEA=(180^{\circ}-\angle B)\div2=(180 - 80)\div2 = 50^{\circ}$。
因为$AD// BC$,所以$\angle BAD+\angle B = 180^{\circ}$,则$\angle BAD=180^{\circ}-\angle B = 100^{\circ}$。
所以$\angle DAE=\angle BAD-\angle BAE=100^{\circ}-50^{\circ}=50^{\circ}$。
【答案】:
(1)证明成立,即$CD = CE$。
(2)$50^{\circ}$
(1)因为四边形$ABCD$是平行四边形,所以$AD// BC$,根据两直线平行,内错角相等,可得$\angle ADE=\angle DEC$。
又因为$DE$是$\angle ADC$的角平分线,所以$\angle ADE=\angle CDE$。
从而$\angle DEC=\angle CDE$,根据等角对等边,可得$CD = CE$。
(2)因为四边形$ABCD$是平行四边形,所以$AB = CD$,$AD// BC$。
由(1)知$CD = CE$,又因为$BE = CE$,所以$AB = BE$。
因为$\angle B = 80^{\circ}$,在$\triangle ABE$中,根据等腰三角形两底角相等,可得$\angle BAE=\angle BEA=(180^{\circ}-\angle B)\div2=(180 - 80)\div2 = 50^{\circ}$。
因为$AD// BC$,所以$\angle BAD+\angle B = 180^{\circ}$,则$\angle BAD=180^{\circ}-\angle B = 100^{\circ}$。
所以$\angle DAE=\angle BAD-\angle BAE=100^{\circ}-50^{\circ}=50^{\circ}$。
【答案】:
(1)证明成立,即$CD = CE$。
(2)$50^{\circ}$
查看更多完整答案,请扫码查看


