勾股定理的逆定理
题设:如果三角形的三边长 $ a $,$ b $,$ c $ 满足
结论:那么这个三角形是直角三角形
应用
判定某一个三角形是否是直角三角形
能够成为直角三角形三边长的三个正整数,称为勾股数
题设:如果三角形的三边长 $ a $,$ b $,$ c $ 满足
$a^{2}+b^{2}=c^{2}$
结论:那么这个三角形是直角三角形
应用
判定某一个三角形是否是直角三角形
能够成为直角三角形三边长的三个正整数,称为勾股数
答案:
【解析】:勾股定理的逆定理是判断一个三角形是否为直角三角形的重要方法,其内容为如果三角形的三边长$a$,$b$,$c$满足$a^{2}+b^{2}=c^{2}$,那么这个三角形是直角三角形,所以此处应填$a^{2}+b^{2}=c^{2}$。
【答案】:$a^{2}+b^{2}=c^{2}$
【答案】:$a^{2}+b^{2}=c^{2}$
1. 五根小棒的长度(单位:cm)分别为 6,7,8,9,10,现从中选择三根,将它们首尾相接摆成三角形,其中能摆成直角三角形的是(
A. 6,7,8
B. 6,8,10
C. 7,8,9
D. 7,9,10
B
).A. 6,7,8
B. 6,8,10
C. 7,8,9
D. 7,9,10
答案:
B
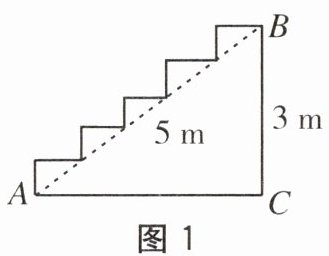
2. 如图 1,在高为 3 m、斜坡长为 5 m 的楼梯表面铺地毯,则地毯的长度至少需要(
A. 3 m
B. 4 m
C. 5 m
D. 7 m
D
).
A. 3 m
B. 4 m
C. 5 m
D. 7 m
答案:
D
3. 如图 2 所示的网格是正方形网格,网格中三条线段的端点均在格点上,以这三条线段为边的三角形是(
A. 锐角
B. 直角
C. 钝角
D. 无法判断
B
)三角形.A. 锐角
B. 直角
C. 钝角
D. 无法判断
答案:
B
4. 如图 3,在正方形 $ ABCD $ 中,$ E $ 为 $ BC $ 的中点,$ CF=\frac{1}{4}CD $,连接 $ AE $,$ AF $,$ EF $,设 $ CF = a $.
(1)线段 $ AE = $
(2)求证:$ AE \perp EF $.

(1)线段 $ AE = $
$2\sqrt{5}a$
,$ AF = $$5a$
,$ EF = $$\sqrt{5}a$
;(用含 $ a $ 的代数式表示)(2)求证:$ AE \perp EF $.

答案:
【解析】:
(1)
因为四边形$ABCD$是正方形,所以$AB = BC = CD = DA$,$\angle B=\angle C=\angle D = 90^{\circ}$。
已知$CF = a$,$CF=\frac{1}{4}CD$,则$CD = 4a$,所以$AB = BC = DA = 4a$,$BE = EC = 2a$,$DF = 3a$。
在$Rt\triangle ABE$中,根据勾股定理$AE=\sqrt{AB^{2}+BE^{2}}=\sqrt{(4a)^{2}+(2a)^{2}}=\sqrt{16a^{2}+4a^{2}}=\sqrt{20a^{2}} = 2\sqrt{5}a$。
在$Rt\triangle ADF$中,根据勾股定理$AF=\sqrt{AD^{2}+DF^{2}}=\sqrt{(4a)^{2}+(3a)^{2}}=\sqrt{16a^{2}+9a^{2}}=\sqrt{25a^{2}} = 5a$。
在$Rt\triangle ECF$中,根据勾股定理$EF=\sqrt{EC^{2}+CF^{2}}=\sqrt{(2a)^{2}+a^{2}}=\sqrt{4a^{2}+a^{2}}=\sqrt{5}a$。
(2)
由(1)可知$AE = 2\sqrt{5}a$,$EF=\sqrt{5}a$,$AF = 5a$。
计算$AE^{2}+EF^{2}=(2\sqrt{5}a)^{2}+(\sqrt{5}a)^{2}=20a^{2}+5a^{2}=25a^{2}$,$AF^{2}=(5a)^{2}=25a^{2}$。
所以$AE^{2}+EF^{2}=AF^{2}$,根据勾股定理的逆定理,可知$\triangle AEF$是直角三角形,且$\angle AEF = 90^{\circ}$,即$AE\perp EF$。
【答案】:
(1)$2\sqrt{5}a$,$5a$,$\sqrt{5}a$
(2)已证$AE\perp EF$
(1)
因为四边形$ABCD$是正方形,所以$AB = BC = CD = DA$,$\angle B=\angle C=\angle D = 90^{\circ}$。
已知$CF = a$,$CF=\frac{1}{4}CD$,则$CD = 4a$,所以$AB = BC = DA = 4a$,$BE = EC = 2a$,$DF = 3a$。
在$Rt\triangle ABE$中,根据勾股定理$AE=\sqrt{AB^{2}+BE^{2}}=\sqrt{(4a)^{2}+(2a)^{2}}=\sqrt{16a^{2}+4a^{2}}=\sqrt{20a^{2}} = 2\sqrt{5}a$。
在$Rt\triangle ADF$中,根据勾股定理$AF=\sqrt{AD^{2}+DF^{2}}=\sqrt{(4a)^{2}+(3a)^{2}}=\sqrt{16a^{2}+9a^{2}}=\sqrt{25a^{2}} = 5a$。
在$Rt\triangle ECF$中,根据勾股定理$EF=\sqrt{EC^{2}+CF^{2}}=\sqrt{(2a)^{2}+a^{2}}=\sqrt{4a^{2}+a^{2}}=\sqrt{5}a$。
(2)
由(1)可知$AE = 2\sqrt{5}a$,$EF=\sqrt{5}a$,$AF = 5a$。
计算$AE^{2}+EF^{2}=(2\sqrt{5}a)^{2}+(\sqrt{5}a)^{2}=20a^{2}+5a^{2}=25a^{2}$,$AF^{2}=(5a)^{2}=25a^{2}$。
所以$AE^{2}+EF^{2}=AF^{2}$,根据勾股定理的逆定理,可知$\triangle AEF$是直角三角形,且$\angle AEF = 90^{\circ}$,即$AE\perp EF$。
【答案】:
(1)$2\sqrt{5}a$,$5a$,$\sqrt{5}a$
(2)已证$AE\perp EF$
查看更多完整答案,请扫码查看


