《2025年新课堂暑假生活北京教育出版社五年级数学》

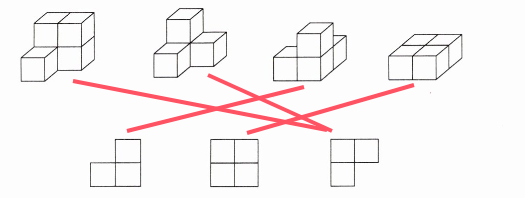
一、连一连。
下面的几何体从上面看到的分别是什么图形？

答案：

二、计算下面各题。
$ \frac { 4 } { 5 } + \frac { 3 } { 4 } $
$ \frac { 4 } { 1 1 } + \frac { 2 } { 5 } + \frac { 7 } { 1 1 } + \frac { 1 } { 5 } $
$ \frac { 4 } { 5 } - \frac { 3 } { 1 0 } + \frac { 2 } { 3 } $
$ \frac { 3 } { 7 } - ( \frac { 9 } { 1 4 } - \frac { 1 } { 2 } ) $
$ \frac { 8 } { 9 } - \frac { 5 } { 9 } + \frac { 1 } { 6 } $
$ \frac { 8 } { 1 5 } + \frac { 2 } { 5 } + \frac { 1 } { 2 } $

答案： 【解析】：
1. $\frac{4}{5} + \frac{3}{4}$，先通分，分母 5 和 4 的最小公倍数是 20，转化为$\frac{16}{20} + \frac{15}{20} = \frac{31}{20}$。
2. $\frac{4}{11} + \frac{2}{5} + \frac{7}{11} + \frac{1}{5}$，利用加法交换律和结合律，$(\frac{4}{11} + \frac{7}{11}) + (\frac{2}{5} + \frac{1}{5}) = 1 + \frac{3}{5} = 1\frac{3}{5}$。
3. $\frac{4}{5} - \frac{3}{10} + \frac{2}{3}$，通分，分母 5、10、3 的最小公倍数是 30，转化为$\frac{24}{30} - \frac{9}{30} + \frac{20}{30} = \frac{35}{30} = \frac{7}{6}$。
4. $\frac{3}{7} - (\frac{9}{14} - \frac{1}{2})$，先算括号内，$\frac{9}{14} - \frac{7}{14} = \frac{2}{14} = \frac{1}{7}$，再算$\frac{3}{7} - \frac{1}{7} = \frac{2}{7}$。
5. $\frac{8}{9} - \frac{5}{9} + \frac{1}{6}$，先算同分母减法，$\frac{3}{9} = \frac{1}{3}$，再算$\frac{1}{3} + \frac{1}{6} = \frac{2}{6} + \frac{1}{6} = \frac{3}{6} = \frac{1}{2}$。
6. $\frac{8}{15} + \frac{2}{5} + \frac{1}{2}$，通分，分母 15、5、2 的最小公倍数是 30，转化为$\frac{16}{30} + \frac{12}{30} + \frac{15}{30} = \frac{43}{30}$。
【答案】：$\frac{31}{20}$，$1\frac{3}{5}$，$\frac{7}{6}$，$\frac{2}{7}$，$\frac{1}{2}$，$\frac{43}{30}$

三、从下面的卡片中任选三个,组出符合要求的三位数。(至少写出3个)

(1)奇数：105、165、501
(2)3的倍数：156、165、516
(3)5的倍数：150、160、105

答案： 【解析】：题目给出的卡片数字为1、5、6、0。
(1) 奇数是指不能被2整除的整数，其个位数字必须是1或5（0、6为偶数，不能在个位）。从给定数字中选三个组成三位数，百位不能为0。当个位是1时，可组成501、601、561、651；当个位是5时，可组成105、605、165、615。
(2) 3的倍数特征是各位数字之和能被3整除。计算各组合数字之和：1+5+6=12（能被3整除），1+5+0=6（能被3整除），5+6+0=11（不能），1+6+0=7（不能）。所以可选数字组合为1、5、6或1、5、0。由1、5、6组成的三位数有156、165、516、561、615、651；由1、5、0组成的三位数有105、150、501、510。
(3) 5的倍数特征是个位数字是0或5。当个位是0时，可组成150、160、510、560、610、650；当个位是5时，可组成105、165、605、615（注意百位不能为0）。
【答案】：
(1)105、165、501
(2)156、165、516
(3)150、160、105