四、根据表格完成复式折线统计图。
下面是某地区一个星期的最高气温和最低气温统计表。
单位:$^{\circ}C$

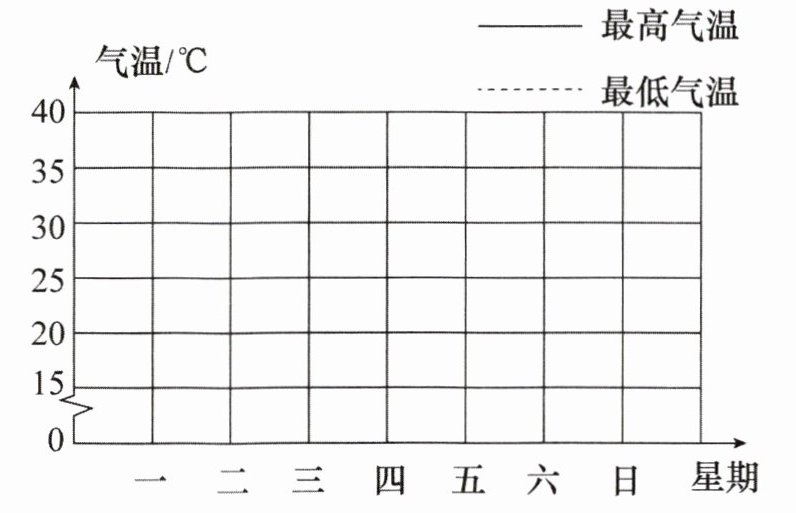
本题可根据统计表中的数据,在复式折线统计图中分别描出最高气温和最低气温对应的点,再依次连接各点即可。
步骤一:确定坐标点
最高气温:星期一$(一,26)$、星期二$(二,27)$、星期三$(三,30)$、星期四$(四,30)$、星期五$(五,31)$、星期六$(六,30)$、星期日$(日,29)$。
最低气温:星期一$(一,20)$、星期二$(二,20)$、星期三$(三,22)$、星期四$(四,22)$、星期五$(五,22)$、星期六$(六,21)$、星期日$(日,20)$。
步骤二:绘制折线
用实线依次连接最高气温对应的坐标点$(一,26)$、$(二,27)$、$(三,30)$、$(四,30)$、$(五,31)$、$(六,30)$、$(日,29)$。
用虚线依次连接最低气温对应的坐标点$(一,20)$、$(二,20)$、$(三,22)$、$(四,22)$、$(五,22)$、$(六,21)$、$(日,20)$。
综上,按照上述步骤即可完成复式折线统计图的绘制。
下面是某地区一个星期的最高气温和最低气温统计表。
单位:$^{\circ}C$


本题可根据统计表中的数据,在复式折线统计图中分别描出最高气温和最低气温对应的点,再依次连接各点即可。
步骤一:确定坐标点
最高气温:星期一$(一,26)$、星期二$(二,27)$、星期三$(三,30)$、星期四$(四,30)$、星期五$(五,31)$、星期六$(六,30)$、星期日$(日,29)$。
最低气温:星期一$(一,20)$、星期二$(二,20)$、星期三$(三,22)$、星期四$(四,22)$、星期五$(五,22)$、星期六$(六,21)$、星期日$(日,20)$。
步骤二:绘制折线
用实线依次连接最高气温对应的坐标点$(一,26)$、$(二,27)$、$(三,30)$、$(四,30)$、$(五,31)$、$(六,30)$、$(日,29)$。
用虚线依次连接最低气温对应的坐标点$(一,20)$、$(二,20)$、$(三,22)$、$(四,22)$、$(五,22)$、$(六,21)$、$(日,20)$。
综上,按照上述步骤即可完成复式折线统计图的绘制。
答案:
本题可根据统计表中的数据,在复式折线统计图中分别描出最高气温和最低气温对应的点,再依次连接各点即可。
步骤一:确定坐标点
最高气温:星期一$(一,26)$、星期二$(二,27)$、星期三$(三,30)$、星期四$(四,30)$、星期五$(五,31)$、星期六$(六,30)$、星期日$(日,29)$。
最低气温:星期一$(一,20)$、星期二$(二,20)$、星期三$(三,22)$、星期四$(四,22)$、星期五$(五,22)$、星期六$(六,21)$、星期日$(日,20)$。
步骤二:绘制折线
用实线依次连接最高气温对应的坐标点$(一,26)$、$(二,27)$、$(三,30)$、$(四,30)$、$(五,31)$、$(六,30)$、$(日,29)$。
用虚线依次连接最低气温对应的坐标点$(一,20)$、$(二,20)$、$(三,22)$、$(四,22)$、$(五,22)$、$(六,21)$、$(日,20)$。
综上,按照上述步骤即可完成复式折线统计图的绘制。
步骤一:确定坐标点
最高气温:星期一$(一,26)$、星期二$(二,27)$、星期三$(三,30)$、星期四$(四,30)$、星期五$(五,31)$、星期六$(六,30)$、星期日$(日,29)$。
最低气温:星期一$(一,20)$、星期二$(二,20)$、星期三$(三,22)$、星期四$(四,22)$、星期五$(五,22)$、星期六$(六,21)$、星期日$(日,20)$。
步骤二:绘制折线
用实线依次连接最高气温对应的坐标点$(一,26)$、$(二,27)$、$(三,30)$、$(四,30)$、$(五,31)$、$(六,30)$、$(日,29)$。
用虚线依次连接最低气温对应的坐标点$(一,20)$、$(二,20)$、$(三,22)$、$(四,22)$、$(五,22)$、$(六,21)$、$(日,20)$。
综上,按照上述步骤即可完成复式折线统计图的绘制。
方块内的数字
如图所示,想一想,图中方块内的数字怎样摆放才能使它们组成一个可以被7除尽的三位数?(提示:方框内的数字可以旋转)
如图所示,想一想,图中方块内的数字怎样摆放才能使它们组成一个可以被7除尽的三位数?(提示:方框内的数字可以旋转)
931
答案:
1. 首先明确数字旋转情况:
数字$6$旋转后可得到$9$。
2. 然后列举所有可能的三位数:
当不旋转$6$时,组成的三位数有$136$,$163$,$316$,$361$,$613$,$631$。
计算$136÷7 = 19\cdots\cdots3$;$163÷7 = 23\cdots\cdots2$;$316÷7 = 45\cdots\cdots1$;$361÷7 = 51\cdots\cdots4$;$613÷7 = 87\cdots\cdots4$;$631÷7 = 90\cdots\cdots1$。
当把$6$旋转为$9$时,组成的三位数有$139$,$193$,$319$,$391$,$913$,$931$。
计算$139÷7 = 19\cdots\cdots6$;$193÷7 = 27\cdots\cdots4$;$319÷7 = 45\cdots\cdots4$;$391÷7 = 55\cdots\cdots6$;$913÷7 = 130\cdots\cdots3$;$931÷7=\frac{931}{7}=133$。
所以方块内数字摆放成$931$(将$6$旋转为$9$,再按$9$,$3$,$1$的顺序排列)能使它们组成一个可以被$7$除尽的三位数。
数字$6$旋转后可得到$9$。
2. 然后列举所有可能的三位数:
当不旋转$6$时,组成的三位数有$136$,$163$,$316$,$361$,$613$,$631$。
计算$136÷7 = 19\cdots\cdots3$;$163÷7 = 23\cdots\cdots2$;$316÷7 = 45\cdots\cdots1$;$361÷7 = 51\cdots\cdots4$;$613÷7 = 87\cdots\cdots4$;$631÷7 = 90\cdots\cdots1$。
当把$6$旋转为$9$时,组成的三位数有$139$,$193$,$319$,$391$,$913$,$931$。
计算$139÷7 = 19\cdots\cdots6$;$193÷7 = 27\cdots\cdots4$;$319÷7 = 45\cdots\cdots4$;$391÷7 = 55\cdots\cdots6$;$913÷7 = 130\cdots\cdots3$;$931÷7=\frac{931}{7}=133$。
所以方块内数字摆放成$931$(将$6$旋转为$9$,再按$9$,$3$,$1$的顺序排列)能使它们组成一个可以被$7$除尽的三位数。
小制作
把一张正方形纸(如图①)沿虚线对折一次得到图②,再沿虚线对折一次得到图③,然后用剪刀沿图③中的虚线(虚线与底边平行)剪去一个角。展开后的图形是

把一张正方形纸(如图①)沿虚线对折一次得到图②,再沿虚线对折一次得到图③,然后用剪刀沿图③中的虚线(虚线与底边平行)剪去一个角。展开后的图形是
剪后图案为一个有两条对称轴的四边形,具体形状为中间有一个正方形缺口的八边形(或描述为:展开后得到一个对称图形,原正方形四个角完整,中间剪去部分展开形成一个小正方形,整体呈现八边形)
。
答案:
剪后图案为一个有两条对称轴的四边形,具体形状为中间有一个正方形缺口的八边形(或描述为:展开后得到一个对称图形,原正方形四个角完整,中间剪去部分展开形成一个小正方形,整体呈现八边形)。
查看更多完整答案,请扫码查看


