《2025年新课堂暑假生活北京教育出版社五年级数学》

2. 把3千克盐分成质量相等的8包,每包的质量是这些盐的几分之几?每包重多少千克?

答案： 【解析】：把3千克盐看作单位“1”，平均分成8包，每包的质量是这些盐的$1÷8 = \frac{1}{8}$；每包的重量为总重量除以包数，即$3÷8 = \frac{3}{8}$千克。
【答案】：$\frac{1}{8}$，$\frac{3}{8}$

四、开动脑筋。
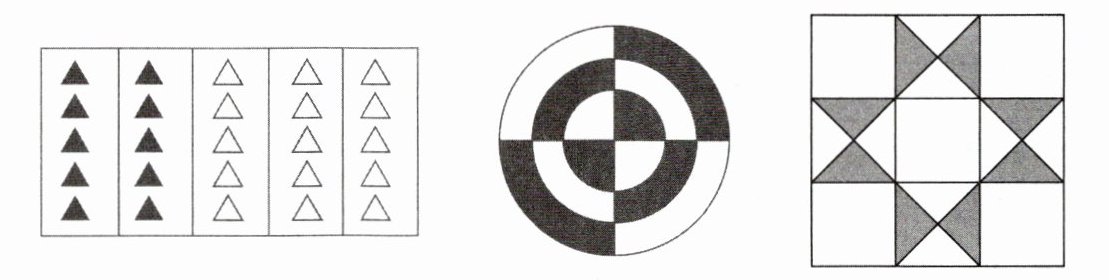
涂色部分是几分之几？

($\frac{2}{5}$)
($\frac{1}{4}$)
($\frac{1}{2}$)

答案： $\frac{2}{5}$，$\frac{1}{4}$，$\frac{1}{2}$

设计纸盒
请你用一张长40cm、宽20cm的长方形红色卡纸,制作一个高是5cm的无盖小纸盒。
情况一：从长方形卡纸四个角剪去边长为5cm的正方形
解：
1. 纸盒长：$40 - 5×2 = $30cm
2. 纸盒宽：$20 - 5×2 = $10cm
3. 纸盒高：5cm
4. 容积：$30×10×5 = $1500cm³
情况二：从长方形卡纸宽边两侧剪去边长为5cm的正方形，剩余部分折叠（以长边为底面周长）
解：
1. 纸盒底面周长（原卡纸长）：40cm
2. 纸盒底面宽：5cm（剪去的正方形边长）
3. 纸盒底面长：$(40 - 5×2)÷2 = $15cm
4. 纸盒高：$20 - 5 = $15cm（原卡纸宽减去剪去部分）
5. 容积：$15×5×15 = $1125cm³
结论
最大容积为1500cm³，对应尺寸：长30cm、宽10cm、高5cm。

答案： 情况一：从长方形卡纸四个角剪去边长为5cm的正方形
解：
1. 纸盒长：$40 - 5×2 = 30\,\text{cm}$
2. 纸盒宽：$20 - 5×2 = 10\,\text{cm}$
3. 纸盒高：$5\,\text{cm}$
4. 容积：$30×10×5 = 1500\,\text{cm}^3$
情况二：从长方形卡纸宽边两侧剪去边长为5cm的正方形，剩余部分折叠（以长边为底面周长）
解：
1. 纸盒底面周长（原卡纸长）：$40\,\text{cm}$
2. 纸盒底面宽：$5\,\text{cm}$（剪去的正方形边长）
3. 纸盒底面长：$(40 - 5×2)÷2 = 15\,\text{cm}$
4. 纸盒高：$20 - 5 = 15\,\text{cm}$（原卡纸宽减去剪去部分）
5. 容积：$15×5×15 = 1125\,\text{cm}^3$
结论
最大容积为$1500\,\text{cm}^3$，对应尺寸：长30cm、宽10cm、高5cm。