《2025年新课堂暑假生活北京教育出版社五年级数学》

一、判断正误。(对的画“√”,错的画“×”)
1. 分数的分母越大,它的分数单位就越小。 (√)
2. 假分数的分子都比分母大。 (×)
3. $4×5= 20$,4 是因数,5 也是因数。 (×)
4. 一个数的因数的个数是有限的。 (√)
5. 个位上是 3、6、9 的数都是 3 的倍数。 (×)

答案： 1.√；2.×；3.×；4.√；5.×

二、连一连。
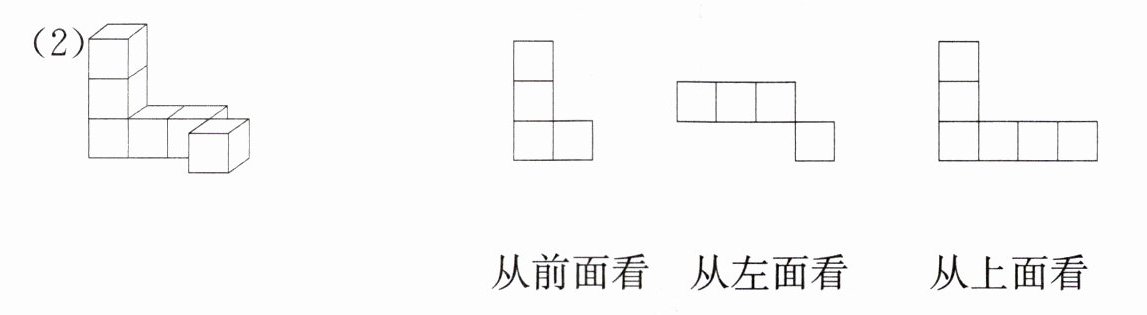
下面的图形是从哪个方向看到的?

（1）第一个图形连从左面看，第二个图形连从前面看，第三个图形连从上面看；（2）第一个图形连从左面看，第二个图形连从上面看，第三个图形连从前面看。

答案： 【解析】：（1）对于第一个立体图形，从前面看，能看到两层，下层有3个小正方形，上层左边有1个小正方形，对应第二个图形；从左面看，能看到两层，下层有2个小正方形，上层左边有1个小正方形，对应第一个图形；从上面看，能看到两行，后面一行有3个小正方形，前面一行左边有1个小正方形，对应第三个图形。
（2）对于第二个立体图形，从前面看，能看到三层，第一层有3个小正方形，第二层左边有1个小正方形，第三层左边有1个小正方形，对应第三个图形；从左面看，能看到三层，每层左边各有1个小正方形，对应第一个图形；从上面看，能看到两行，前面一行有3个小正方形，后面一行右边有1个小正方形，对应第二个图形。
【答案】：（1）第一个图形连从左面看，第二个图形连从前面看，第三个图形连从上面看；（2）第一个图形连从左面看，第二个图形连从上面看，第三个图形连从前面看。

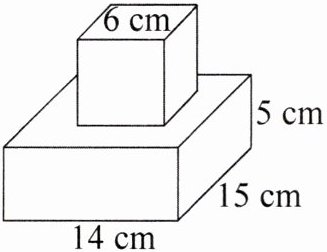
三、如图,在一个长方体上面放了一个正方体,计算这个几何体的体积。

1266

答案： 【解析】：该几何体由一个长方体和一个正方体组成，体积为两者体积之和。长方体的长、宽、高分别为14cm、15cm、5cm，根据长方体体积公式$V = 长×宽×高$，其体积为$14×15×5$。正方体的棱长为6cm，根据正方体体积公式$V = 棱长×棱长×棱长$，其体积为$6×6×6$。将两者体积相加可得总体积。
计算过程如下：
长方体体积：$14×15×5 = 1050$（$cm^3$）
正方体体积：$6×6×6 = 216$（$cm^3$）
总体积：$1050 + 216 = 1266$（$cm^3$）
【答案】：1266