6. 如图,在▱ABCD中,$AD= 6$,$AB= 4$,$DE平分∠ADC$交 BC 于点 E,则 BE 的长是 ()

A. 2
B. 3
C. 4
D. 5

A. 2
B. 3
C. 4
D. 5
答案:
A
1. 如图,在▱ABCD中,对角线 AC,BD 相交于点 O,点 E,F 分别是边 AD,AB 上的点,连接 OE,OF,EF. 若$AB= 7$,$BC= 5\sqrt {2}$,$∠DAB= 45^{\circ }$,则$\triangle OEF$周长的最小值是____.
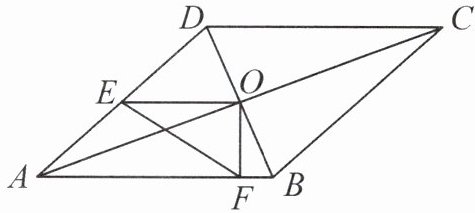

答案:
$\sqrt{37}$
2. 如图,在▱ABCD中,点 E 在 CD 边上运动(不与 C,D 两点重合),连接 AE 并延长与 BC 的延长线交于点 F. 连接 BE,DF,若$\triangle BCE$的面积为 8,则$\triangle DEF$的面积为____.


答案:
$8$
3. 如图,在▱ABCD中,$AB= 6cm$,$∠BCD$的平分线交 AD 于点 E,则$DE= $____.
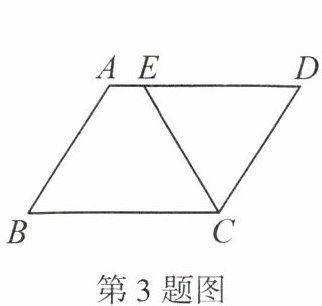

答案:
$6cm$
4. 如图,把平行四边形 ABCD 折叠,使点 C 与点 A 重合,这时点 D 落在点$D_{1}$处,折痕为 EF,若$∠BAE= 55^{\circ }$,则$∠D_{1}AD= $____.


答案:
$55^{\circ}$
1. 在$\triangle ABC$中,$AB= AC$,点 D 在边 BC 所在的直线上,过点 D 作$DF// AC$交直线 AB 于点 F,$DE// AB$交直线 AC 于点 E.
(1)当点 D 在边 BC 上时,如图①,求证:$DE+DF= AC$;
(2)当点 D 在边 BC 的延长线上时,如图②,当点 D 在边 BC 的反向延长线上时,如图③,请分别写出图②、图③中 DE,DF,AC 之间的数量关系,不需要证明;
(3)若$AC= 6$,$DE= 4$,则$DF= $____.

(1)当点 D 在边 BC 上时,如图①,求证:$DE+DF= AC$;
(2)当点 D 在边 BC 的延长线上时,如图②,当点 D 在边 BC 的反向延长线上时,如图③,请分别写出图②、图③中 DE,DF,AC 之间的数量关系,不需要证明;
(3)若$AC= 6$,$DE= 4$,则$DF= $____.

答案:
【解析】:
(1)
因为$DF// AC$,$DE// AB$,所以四边形$AFDE$是平行四边形,所以$DF = AE$。
又因为$DE// AB$,所以$\angle B=\angle EDC$。
因为$AB = AC$,所以$\angle B=\angle C$,则$\angle C=\angle EDC$,所以$DE = EC$。
所以$DE + DF=EC + AE=AC$。
(2)
图②:
因为$DF// AC$,$DE// AB$,所以四边形$AFDE$是平行四边形,所以$DF = AE$。
因为$DE// AB$,所以$\angle ABC=\angle EDC$。
因为$AB = AC$,所以$\angle ABC=\angle ACB=\angle ECD$,则$\angle EDC=\angle ECD$,所以$DE = EC$。
$AC=AE - EC$,即$AC=DF - DE$。
图③:
因为$DF// AC$,$DE// AB$,所以四边形$AFDE$是平行四边形,所以$DE = AF$。
因为$DF// AC$,所以$\angle FDB=\angle C$。
因为$AB = AC$,所以$\angle ABC=\angle C$,又$\angle ABC=\angle FBD$,则$\angle FDB=\angle FBD$,所以$DF = BF$。
$AC=AB = BF - AF$,即$AC=DE - DF$。
(3)
当如图①的情况时,$DF=AC - DE$,已知$AC = 6$,$DE = 4$,则$DF=6 - 4=2$。
当如图②的情况时,$DF=AC + DE$,已知$AC = 6$,$DE = 4$,则$DF=6 + 4=10$。
【答案】:
(1) 证明如上;
(2) 图②:$AC=DF - DE$;图③:$AC=DE - DF$;
(3) $2$或$10$。
(1)
因为$DF// AC$,$DE// AB$,所以四边形$AFDE$是平行四边形,所以$DF = AE$。
又因为$DE// AB$,所以$\angle B=\angle EDC$。
因为$AB = AC$,所以$\angle B=\angle C$,则$\angle C=\angle EDC$,所以$DE = EC$。
所以$DE + DF=EC + AE=AC$。
(2)
图②:
因为$DF// AC$,$DE// AB$,所以四边形$AFDE$是平行四边形,所以$DF = AE$。
因为$DE// AB$,所以$\angle ABC=\angle EDC$。
因为$AB = AC$,所以$\angle ABC=\angle ACB=\angle ECD$,则$\angle EDC=\angle ECD$,所以$DE = EC$。
$AC=AE - EC$,即$AC=DF - DE$。
图③:
因为$DF// AC$,$DE// AB$,所以四边形$AFDE$是平行四边形,所以$DE = AF$。
因为$DF// AC$,所以$\angle FDB=\angle C$。
因为$AB = AC$,所以$\angle ABC=\angle C$,又$\angle ABC=\angle FBD$,则$\angle FDB=\angle FBD$,所以$DF = BF$。
$AC=AB = BF - AF$,即$AC=DE - DF$。
(3)
当如图①的情况时,$DF=AC - DE$,已知$AC = 6$,$DE = 4$,则$DF=6 - 4=2$。
当如图②的情况时,$DF=AC + DE$,已知$AC = 6$,$DE = 4$,则$DF=6 + 4=10$。
【答案】:
(1) 证明如上;
(2) 图②:$AC=DF - DE$;图③:$AC=DE - DF$;
(3) $2$或$10$。
2. 如图,在四边形 ABCD 中,$AD// BC$,点 E,F 分别在 AD,BC 上,$AE= CF$,过点 A,C 分别作 EF 的垂线,垂足分别为 G,H.
(1)求证:$\triangle AGE\cong \triangle CHF$;
(2)连接 AC,线段 GH 与 AC 是否互相平分? 请说明理由.

(1)求证:$\triangle AGE\cong \triangle CHF$;
(2)连接 AC,线段 GH 与 AC 是否互相平分? 请说明理由.

答案:
1. (1)证明:因为$AD// BC$,所以$\angle AEG=\angle CFH$。
又因为$AG\perp EF$,$CH\perp EF$,所以$\angle AGE = \angle CHF = 90^{\circ}$。
已知$AE = CF$,在$\triangle AGE$和$\triangle CHF$中,$\begin{cases}\angle AGE=\angle CHF\\\angle AEG = \angle CFH\\AE = CF\end{cases}$,所以$\triangle AGE\cong \triangle CHF(AAS)$。
2. (2)线段$GH$与$AC$互相平分。理由如下:
连接$AH$,$CG$。
因为$\triangle AGE\cong \triangle CHF$,所以$AG = CH$。
又因为$AG\perp EF$,$CH\perp EF$,所以$AG// CH$。
所以四边形$AHCG$是平行四边形。
因为平行四边形的对角线互相平分,所以$GH$与$AC$互相平分。
又因为$AG\perp EF$,$CH\perp EF$,所以$\angle AGE = \angle CHF = 90^{\circ}$。
已知$AE = CF$,在$\triangle AGE$和$\triangle CHF$中,$\begin{cases}\angle AGE=\angle CHF\\\angle AEG = \angle CFH\\AE = CF\end{cases}$,所以$\triangle AGE\cong \triangle CHF(AAS)$。
2. (2)线段$GH$与$AC$互相平分。理由如下:
连接$AH$,$CG$。
因为$\triangle AGE\cong \triangle CHF$,所以$AG = CH$。
又因为$AG\perp EF$,$CH\perp EF$,所以$AG// CH$。
所以四边形$AHCG$是平行四边形。
因为平行四边形的对角线互相平分,所以$GH$与$AC$互相平分。
查看更多完整答案,请扫码查看


