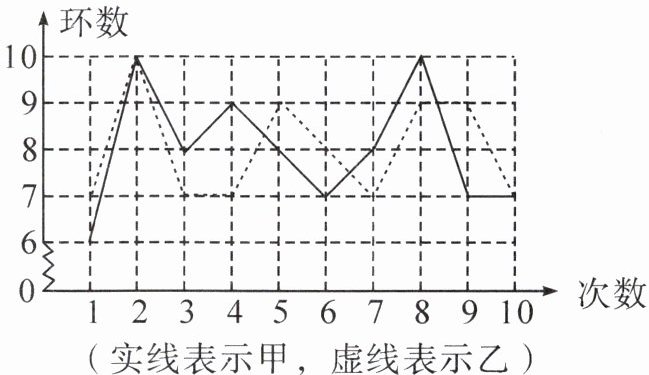
2. 甲、乙两名射击运动员进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示。
根据图中信息,回答下列问题:
(1)甲的平均数是______,乙的中位数是______;
(2)分别计算甲、乙成绩的方差,从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
(实线表示甲,虚线表示乙)
根据图中信息,回答下列问题:
(1)甲的平均数是______,乙的中位数是______;
(2)分别计算甲、乙成绩的方差,从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
(实线表示甲,虚线表示乙)

答案:
【解析】:
### (1)计算甲的平均数和乙的中位数
**计算甲的平均数:**
根据平均数公式$\bar{x}=\frac{x_{1}+x_{2}+\cdots +x_{n}}{n}$(其中$n$是数据个数,$x_{i}$是第$i$个数据)。
甲射击$10$次的成绩分别为$6$、$10$、$8$、$9$、$8$、$7$、$8$、$10$、$7$、$7$。
则甲的平均数$\bar{x}_{甲}=\frac{6 + 10 + 8 + 9 + 8 + 7 + 8 + 10 + 7 + 7}{10}=\frac{80}{10}=8$。
**计算乙的中位数:**
将乙射击$10$次的成绩(从小到大排列):$7$、$7$、$7$、$7$、$8$、$8$、$9$、$9$、$9$、$10$。
中位数是按顺序排列的一组数据中居于中间位置的数,如果数据有奇数个,则正中间的数字为中位数;如果数据有偶数个,则中间两位数的平均数为中位数。
这里$n = 10$(偶数),所以乙的中位数是$\frac{8 + 8}{2}=7.5$。
### (2)计算甲、乙成绩的方差并比较稳定性
**计算甲成绩的方差:**
根据方差公式$s^{2}=\frac{1}{n}[(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+\cdots+(x_{n}-\bar{x})^{2}]$。
$\bar{x}_{甲}=8$,$n = 10$。
$(6 - 8)^{2}+(10 - 8)^{2}+(8 - 8)^{2}+(9 - 8)^{2}+(8 - 8)^{2}+(7 - 8)^{2}+(8 - 8)^{2}+(10 - 8)^{2}+(7 - 8)^{2}+(7 - 8)^{2}$
$=(-2)^{2}+2^{2}+0^{2}+1^{2}+0^{2}+(-1)^{2}+0^{2}+2^{2}+(-1)^{2}+(-1)^{2}$
$=4 + 4+0 + 1+0 + 1+0 + 4+1 + 1=16$。
则$s_{甲}^{2}=\frac{16}{10}=1.6$。
**计算乙成绩的平均数:**
乙射击$10$次的成绩分别为$7$、$7$、$7$、$7$、$8$、$8$、$9$、$9$、$9$、$10$。
$\bar{x}_{乙}=\frac{7 + 7 + 7 + 7 + 8 + 8 + 9 + 9 + 9 + 10}{10}=\frac{80}{10}=8$。
**计算乙成绩的方差:**
$(7 - 8)^{2}+(7 - 8)^{2}+(7 - 8)^{2}+(7 - 8)^{2}+(8 - 8)^{2}+(8 - 8)^{2}+(9 - 8)^{2}+(9 - 8)^{2}+(9 - 8)^{2}+(10 - 8)^{2}$
$=(-1)^{2}+(-1)^{2}+(-1)^{2}+(-1)^{2}+0^{2}+0^{2}+1^{2}+1^{2}+1^{2}+2^{2}$
$=1 + 1+1 + 1+0 + 0+1 + 1+1 + 4 = 12$。
则$s_{乙}^{2}=\frac{12}{10}=1.2$。
因为方差越小,数据的波动越小,成绩越稳定,$s_{甲}^{2}=1.6$,$s_{乙}^{2}=1.2$,$s_{甲}^{2}>s_{乙}^{2}$,所以乙运动员的射击成绩更稳定。
【答案】:
(1)$8$;$7.5$
(2)甲成绩的方差$s_{甲}^{2}=1.6$,乙成绩的方差$s_{乙}^{2}=1.2$,乙运动员的射击成绩更稳定。
### (1)计算甲的平均数和乙的中位数
**计算甲的平均数:**
根据平均数公式$\bar{x}=\frac{x_{1}+x_{2}+\cdots +x_{n}}{n}$(其中$n$是数据个数,$x_{i}$是第$i$个数据)。
甲射击$10$次的成绩分别为$6$、$10$、$8$、$9$、$8$、$7$、$8$、$10$、$7$、$7$。
则甲的平均数$\bar{x}_{甲}=\frac{6 + 10 + 8 + 9 + 8 + 7 + 8 + 10 + 7 + 7}{10}=\frac{80}{10}=8$。
**计算乙的中位数:**
将乙射击$10$次的成绩(从小到大排列):$7$、$7$、$7$、$7$、$8$、$8$、$9$、$9$、$9$、$10$。
中位数是按顺序排列的一组数据中居于中间位置的数,如果数据有奇数个,则正中间的数字为中位数;如果数据有偶数个,则中间两位数的平均数为中位数。
这里$n = 10$(偶数),所以乙的中位数是$\frac{8 + 8}{2}=7.5$。
### (2)计算甲、乙成绩的方差并比较稳定性
**计算甲成绩的方差:**
根据方差公式$s^{2}=\frac{1}{n}[(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+\cdots+(x_{n}-\bar{x})^{2}]$。
$\bar{x}_{甲}=8$,$n = 10$。
$(6 - 8)^{2}+(10 - 8)^{2}+(8 - 8)^{2}+(9 - 8)^{2}+(8 - 8)^{2}+(7 - 8)^{2}+(8 - 8)^{2}+(10 - 8)^{2}+(7 - 8)^{2}+(7 - 8)^{2}$
$=(-2)^{2}+2^{2}+0^{2}+1^{2}+0^{2}+(-1)^{2}+0^{2}+2^{2}+(-1)^{2}+(-1)^{2}$
$=4 + 4+0 + 1+0 + 1+0 + 4+1 + 1=16$。
则$s_{甲}^{2}=\frac{16}{10}=1.6$。
**计算乙成绩的平均数:**
乙射击$10$次的成绩分别为$7$、$7$、$7$、$7$、$8$、$8$、$9$、$9$、$9$、$10$。
$\bar{x}_{乙}=\frac{7 + 7 + 7 + 7 + 8 + 8 + 9 + 9 + 9 + 10}{10}=\frac{80}{10}=8$。
**计算乙成绩的方差:**
$(7 - 8)^{2}+(7 - 8)^{2}+(7 - 8)^{2}+(7 - 8)^{2}+(8 - 8)^{2}+(8 - 8)^{2}+(9 - 8)^{2}+(9 - 8)^{2}+(9 - 8)^{2}+(10 - 8)^{2}$
$=(-1)^{2}+(-1)^{2}+(-1)^{2}+(-1)^{2}+0^{2}+0^{2}+1^{2}+1^{2}+1^{2}+2^{2}$
$=1 + 1+1 + 1+0 + 0+1 + 1+1 + 4 = 12$。
则$s_{乙}^{2}=\frac{12}{10}=1.2$。
因为方差越小,数据的波动越小,成绩越稳定,$s_{甲}^{2}=1.6$,$s_{乙}^{2}=1.2$,$s_{甲}^{2}>s_{乙}^{2}$,所以乙运动员的射击成绩更稳定。
【答案】:
(1)$8$;$7.5$
(2)甲成绩的方差$s_{甲}^{2}=1.6$,乙成绩的方差$s_{乙}^{2}=1.2$,乙运动员的射击成绩更稳定。
3. 我市某中学举行“中国梦·校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛。两个队各选出的5名选手的决赛成绩如图所示。

(1)根据图示填写下表:

(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手的成绩较为稳定。

(1)根据图示填写下表:

(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手的成绩较为稳定。
答案:
【解析】:
(1) 初中代表队平均数:$(75 + 80 + 85 + 85 + 100)\div5 = 85$(分),众数是$85$分;高中代表队成绩从小到大排列为$70$,$75$,$80$,$100$,$100$,中位数是$80$分。
(2) 平均数相同,初中队中位数$85$分大于高中队中位数$80$分,所以初中队成绩较好。
(3) 初中队方差$S_{初中}^{2}=\frac{1}{5}[(75 - 85)^{2}+(80 - 85)^{2}+(85 - 85)^{2}+(85 - 85)^{2}+(100 - 85)^{2}] = 70$;高中队方差$S_{高中}^{2}=\frac{1}{5}[(70 - 85)^{2}+(75 - 85)^{2}+(80 - 85)^{2}+(100 - 85)^{2}+(100 - 85)^{2}] = 160$。方差越小成绩越稳定,所以初中代表队选手成绩较为稳定。
【答案】:
(1) $85$;$85$;$80$
(2) 初中队
(3) 初中队方差$70$,高中队方差$160$,初中代表队
(1) 初中代表队平均数:$(75 + 80 + 85 + 85 + 100)\div5 = 85$(分),众数是$85$分;高中代表队成绩从小到大排列为$70$,$75$,$80$,$100$,$100$,中位数是$80$分。
(2) 平均数相同,初中队中位数$85$分大于高中队中位数$80$分,所以初中队成绩较好。
(3) 初中队方差$S_{初中}^{2}=\frac{1}{5}[(75 - 85)^{2}+(80 - 85)^{2}+(85 - 85)^{2}+(85 - 85)^{2}+(100 - 85)^{2}] = 70$;高中队方差$S_{高中}^{2}=\frac{1}{5}[(70 - 85)^{2}+(75 - 85)^{2}+(80 - 85)^{2}+(100 - 85)^{2}+(100 - 85)^{2}] = 160$。方差越小成绩越稳定,所以初中代表队选手成绩较为稳定。
【答案】:
(1) $85$;$85$;$80$
(2) 初中队
(3) 初中队方差$70$,高中队方差$160$,初中代表队
查看更多完整答案,请扫码查看


