2. 中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图.
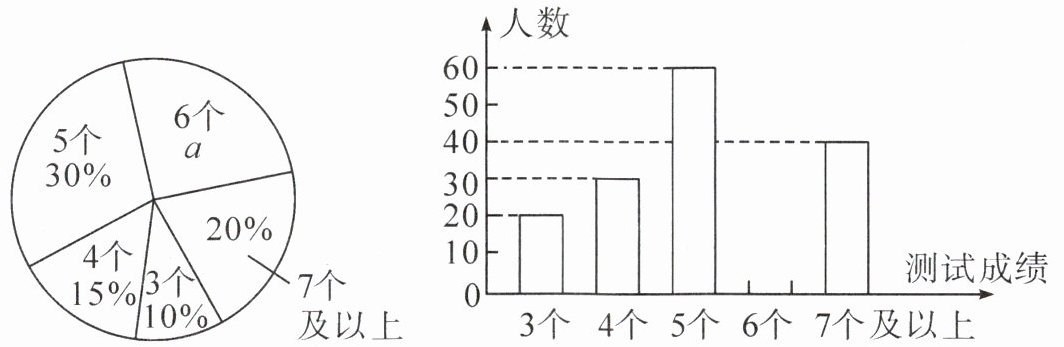
请你根据图中的信息,解答下列问题:
(1)写出扇形图中$a= $____%,并补全条形统计图;
(2)在这次抽测中,测试成绩的众数和中位数分别是多少?
(3)该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名.

请你根据图中的信息,解答下列问题:
(1)写出扇形图中$a= $____%,并补全条形统计图;
(2)在这次抽测中,测试成绩的众数和中位数分别是多少?
(3)该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名.
答案:
【解析】:
(1) 因为扇形统计图中各部分百分比之和为$100\%$,所以$a = 100\%-(30\% + 15\%+10\% + 20\%)=25\%$。
已知做$5$个的人数占$30\%$,且人数为$60$人,那么总人数为$60\div30\% = 200$人。
做$6$个的人数为$200\times25\% = 50$人,补全条形统计图(略)。
(2) 众数是一组数据中出现次数最多的数据。在这组数据中,$5$个出现的次数最多($60$人),所以众数是$5$个。
将数据从小到大排列:$3$个、$4$个、$5$个、$6$个、$7$个及以上。总人数$n = 200$(偶数),中位数是第$\frac{n}{2}=100$个数和第$\frac{n}{2}+1 = 101$个数的平均数。
前两组人数:$20 + 30=50$人,前三组人数:$20 + 30+60 = 110$人,所以第$100$个数和第$101$个数都在$5$个这一组,中位数是$5$个。
(3) 达$6$个以上(含$6$个)的百分比为$25\%+20\%=45\%$。
该区选报引体向上的男生共有$1800$人,能获得满分的人数为$1800\times45\%=810$人。
【答案】:
(1)$25$
(2)众数是$5$个,中位数是$5$个
(3)$810$名
(1) 因为扇形统计图中各部分百分比之和为$100\%$,所以$a = 100\%-(30\% + 15\%+10\% + 20\%)=25\%$。
已知做$5$个的人数占$30\%$,且人数为$60$人,那么总人数为$60\div30\% = 200$人。
做$6$个的人数为$200\times25\% = 50$人,补全条形统计图(略)。
(2) 众数是一组数据中出现次数最多的数据。在这组数据中,$5$个出现的次数最多($60$人),所以众数是$5$个。
将数据从小到大排列:$3$个、$4$个、$5$个、$6$个、$7$个及以上。总人数$n = 200$(偶数),中位数是第$\frac{n}{2}=100$个数和第$\frac{n}{2}+1 = 101$个数的平均数。
前两组人数:$20 + 30=50$人,前三组人数:$20 + 30+60 = 110$人,所以第$100$个数和第$101$个数都在$5$个这一组,中位数是$5$个。
(3) 达$6$个以上(含$6$个)的百分比为$25\%+20\%=45\%$。
该区选报引体向上的男生共有$1800$人,能获得满分的人数为$1800\times45\%=810$人。
【答案】:
(1)$25$
(2)众数是$5$个,中位数是$5$个
(3)$810$名
查看更多完整答案,请扫码查看


