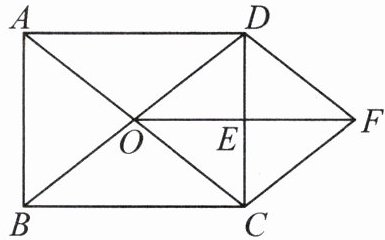
1. 如图,在矩形 $A B C D$ 中,已知对角线 $A C, B D$ 相交于点 $O, E$ 是 $C D$ 的中点,连接 $O E$. 过点 $C$ 作 $C F / / B D$ 交线段 $O E$ 的延长线于点 $F$, 连接 $D F$. 求证:
(1) $\triangle O D E \cong \triangle F C E$;
(2) 四边形 $O D F C$ 是菱形.
(1) $\triangle O D E \cong \triangle F C E$;
(2) 四边形 $O D F C$ 是菱形.

答案:
【解析】:
(1) 因为$CF// BD$,所以$\angle DOE=\angle CFE$。
又因为$E$是$CD$的中点,所以$DE = CE$。
在$\triangle ODE$和$\triangle FCE$中,$\left\{\begin{array}{l}\angle DOE=\angle CFE\\\angle DEO=\angle CEF\\DE = CE\end{array}\right.$(对顶角相等),根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ODE\cong\triangle FCE$。
(2) 由$\triangle ODE\cong\triangle FCE$,可得$OD = FC$。
因为$CF// BD$,即$FC// OD$,所以四边形$ODFC$是平行四边形。
在矩形$ABCD$中,$OC = OD$(矩形的对角线相等且互相平分)。
一组邻边相等的平行四边形是菱形,所以平行四边形$ODFC$是菱形。
【答案】:
(1) $\triangle ODE\cong\triangle FCE$(证明过程见解析);
(2) 四边形$ODFC$是菱形(证明过程见解析)。
(1) 因为$CF// BD$,所以$\angle DOE=\angle CFE$。
又因为$E$是$CD$的中点,所以$DE = CE$。
在$\triangle ODE$和$\triangle FCE$中,$\left\{\begin{array}{l}\angle DOE=\angle CFE\\\angle DEO=\angle CEF\\DE = CE\end{array}\right.$(对顶角相等),根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ODE\cong\triangle FCE$。
(2) 由$\triangle ODE\cong\triangle FCE$,可得$OD = FC$。
因为$CF// BD$,即$FC// OD$,所以四边形$ODFC$是平行四边形。
在矩形$ABCD$中,$OC = OD$(矩形的对角线相等且互相平分)。
一组邻边相等的平行四边形是菱形,所以平行四边形$ODFC$是菱形。
【答案】:
(1) $\triangle ODE\cong\triangle FCE$(证明过程见解析);
(2) 四边形$ODFC$是菱形(证明过程见解析)。
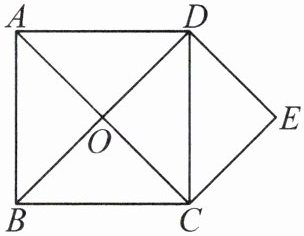
2. 如图,正方形 $A B C D$ 的对角线 $A C$ 与 $B D$ 交于点 $O$, 分别过点 $C$、点 $D$ 作 $C E / / B D$, $D E / / A C$.
求证: (1) 四边形 $O C E D$ 是正方形;
(2) 若 $A B= 4$, 求正方形 $O C E D$ 的面积.
求证: (1) 四边形 $O C E D$ 是正方形;
(2) 若 $A B= 4$, 求正方形 $O C E D$ 的面积.

答案:
【解析】:
(1) 因为$CE// BD$,$DE// AC$,所以四边形$OCED$是平行四边形。
又因为正方形$ABCD$中,$AC\perp BD$,即$\angle DOC = 90^{\circ}$,$OD = OC$。
有一个角是直角的平行四边形是矩形,一组邻边相等的矩形是正方形,所以四边形$OCED$是正方形。
(2) 因为正方形$ABCD$中,$AB = 4$,根据勾股定理$AC=\sqrt{AB^{2}+BC^{2}}$($AB = BC = 4$),可得$AC=\sqrt{4^{2}+4^{2}}=\sqrt{32}=4\sqrt{2}$。
因为正方形$ABCD$的对角线$AC$、$BD$相交于点$O$,所以$OC=\dfrac{1}{2}AC$,则$OC = 2\sqrt{2}$。
因为四边形$OCED$是正方形,根据正方形面积公式$S = a^{2}$($a$为边长),这里$a = OC$,所以正方形$OCED$的面积$S=(2\sqrt{2})^{2}=8$。
【答案】:
(1) 证明过程如上述解析,证得四边形$OCED$是正方形。
(2) 正方形$OCED$的面积为$8$。
(1) 因为$CE// BD$,$DE// AC$,所以四边形$OCED$是平行四边形。
又因为正方形$ABCD$中,$AC\perp BD$,即$\angle DOC = 90^{\circ}$,$OD = OC$。
有一个角是直角的平行四边形是矩形,一组邻边相等的矩形是正方形,所以四边形$OCED$是正方形。
(2) 因为正方形$ABCD$中,$AB = 4$,根据勾股定理$AC=\sqrt{AB^{2}+BC^{2}}$($AB = BC = 4$),可得$AC=\sqrt{4^{2}+4^{2}}=\sqrt{32}=4\sqrt{2}$。
因为正方形$ABCD$的对角线$AC$、$BD$相交于点$O$,所以$OC=\dfrac{1}{2}AC$,则$OC = 2\sqrt{2}$。
因为四边形$OCED$是正方形,根据正方形面积公式$S = a^{2}$($a$为边长),这里$a = OC$,所以正方形$OCED$的面积$S=(2\sqrt{2})^{2}=8$。
【答案】:
(1) 证明过程如上述解析,证得四边形$OCED$是正方形。
(2) 正方形$OCED$的面积为$8$。
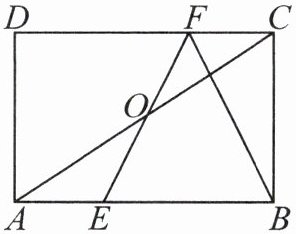
3. 如图,在矩形 $A B C D$ 中, $E, F$ 分别是 $A B, C D$ 上的点, $A E= C F$, 连接 $E F, B F, E F$ 与对角线 $A C$ 交于点 $O$, 且 $B E= B F, \angle B E F= 2 \angle B A C$.
(1) 求证: $O E= O F$;
(2) 若 $B C= 2 \sqrt{3}$, 求 $A B$ 的长.
(1) 求证: $O E= O F$;
(2) 若 $B C= 2 \sqrt{3}$, 求 $A B$ 的长.

答案:
【解析】:
(1) 因为四边形$ABCD$是矩形,所以$AB// CD$。
根据两直线平行,内错角相等,可得$\angle OAE=\angle OCF$。
在$\triangle AOE$和$\triangle COF$中,$\left\{\begin{array}{l}\angle OAE = \angle OCF\\\angle AOE=\angle COF\\AE = CF\end{array}\right.$($AAS$判定定理)。
所以$\triangle AOE\cong\triangle COF$,则$OE = OF$。
(2) 连接$OB$。
因为$BE = BF$,$OE = OF$,根据等腰三角形三线合一,所以$BO\perp EF$。
又因为$\angle BEF = 2\angle BAC$,$\angle BEF=\angle BAC+\angle AOE$,所以$\angle BAC=\angle AOE$。
则$AE = OE$,因为$AE = CF$,$OE = OF$,所以$OF = CF$。
因为$AB// CD$,所以$\angle OCF=\angle BAC$,又$\angle BAC=\angle AOE=\angle COF$,所以$\angle OCF=\angle COF$,则$OF = CF$。
设$AE = x$,则$OE = x$,$OF = x$,$CF = x$,$BE = BF$,$AB = CD$,$AB=AE + BE$,$CD=CF + DF$,所以$BE = DF$。
因为四边形$ABCD$是矩形,所以$\angle ABC = 90^{\circ}$,$BO$是$EF$的中垂线,所以$\angle OBC = 30^{\circ}$。
已知$BC = 2\sqrt{3}$,在$Rt\triangle ABC$中,$\tan\angle BAC=\frac{BC}{AB}$,又因为$\angle BAC = 30^{\circ}$,$\tan30^{\circ}=\frac{\sqrt{3}}{3}$,$BC = 2\sqrt{3}$。
根据$\tan\angle BAC=\frac{BC}{AB}$,可得$AB=\frac{BC}{\tan\angle BAC}=\frac{2\sqrt{3}}{\frac{\sqrt{3}}{3}} = 6$。
【答案】:
(1) 证明过程如上述解析,证得$OE = OF$。
(2)$AB$的长为$6$。
(1) 因为四边形$ABCD$是矩形,所以$AB// CD$。
根据两直线平行,内错角相等,可得$\angle OAE=\angle OCF$。
在$\triangle AOE$和$\triangle COF$中,$\left\{\begin{array}{l}\angle OAE = \angle OCF\\\angle AOE=\angle COF\\AE = CF\end{array}\right.$($AAS$判定定理)。
所以$\triangle AOE\cong\triangle COF$,则$OE = OF$。
(2) 连接$OB$。
因为$BE = BF$,$OE = OF$,根据等腰三角形三线合一,所以$BO\perp EF$。
又因为$\angle BEF = 2\angle BAC$,$\angle BEF=\angle BAC+\angle AOE$,所以$\angle BAC=\angle AOE$。
则$AE = OE$,因为$AE = CF$,$OE = OF$,所以$OF = CF$。
因为$AB// CD$,所以$\angle OCF=\angle BAC$,又$\angle BAC=\angle AOE=\angle COF$,所以$\angle OCF=\angle COF$,则$OF = CF$。
设$AE = x$,则$OE = x$,$OF = x$,$CF = x$,$BE = BF$,$AB = CD$,$AB=AE + BE$,$CD=CF + DF$,所以$BE = DF$。
因为四边形$ABCD$是矩形,所以$\angle ABC = 90^{\circ}$,$BO$是$EF$的中垂线,所以$\angle OBC = 30^{\circ}$。
已知$BC = 2\sqrt{3}$,在$Rt\triangle ABC$中,$\tan\angle BAC=\frac{BC}{AB}$,又因为$\angle BAC = 30^{\circ}$,$\tan30^{\circ}=\frac{\sqrt{3}}{3}$,$BC = 2\sqrt{3}$。
根据$\tan\angle BAC=\frac{BC}{AB}$,可得$AB=\frac{BC}{\tan\angle BAC}=\frac{2\sqrt{3}}{\frac{\sqrt{3}}{3}} = 6$。
【答案】:
(1) 证明过程如上述解析,证得$OE = OF$。
(2)$AB$的长为$6$。
查看更多完整答案,请扫码查看


