《2025年快乐暑假天天练八年级数学》

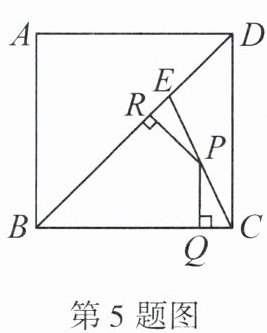
5. 如图, $E$ 是边长为 4 的正方形 $ABCD$ 的对角线 $BD$ 上的一点,且 $B E= B C, P$ 为 $C E$ 上任意一点, $P Q \perp B C$ 于点 $Q, P R \perp B R$ 于点 $R$, 则 $P Q+P R$ 的值是 ()

A. $2 \sqrt{2}$
B. 2
C. $2 \sqrt{3}$
D. $\frac{8}{3}$

答案： A

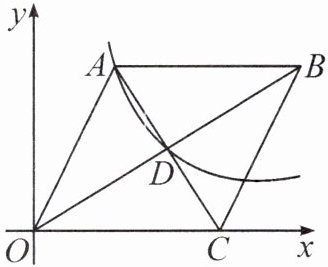
6. 如图,平行四边形 $O A B C$ 的顶点 $C$ 在 $x$ 轴的正半轴上,顶点 $A$, $B$ 在第一象限内,且点 $A$ 的横坐标为 2 , 对角线 $A C$ 与 $O B$ 交于点 $D$, 若反比例函数 $y= \frac{10}{x}$ 的图象经过点 $A$ 与点 $D$, 则平行四边形 $O A B C$ 的面积为 ()

A. 30
B. 24
C. 20
D. 16

答案： A

1. 已知菱形 $A B C D$ 的面积为 $24 \mathrm{~cm}^2$, 若对角线 $A C= 6 \mathrm{~cm}$, 则这个菱形的边长为______ $\mathrm{cm}$.

答案： 1. $5$

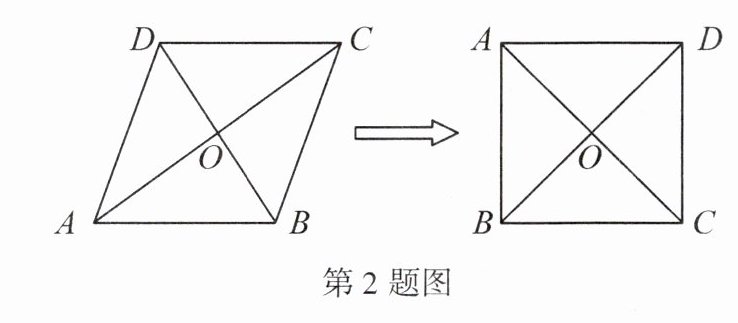
2. 如图,菱形 $A B C D$ 的对角线交于点 $O$, 请你添加一个条件:______, 使得该菱形成为正方形. (只填一个条件)

答案： $\angle ABC = 90^{\circ}$（或$AC = BD$）

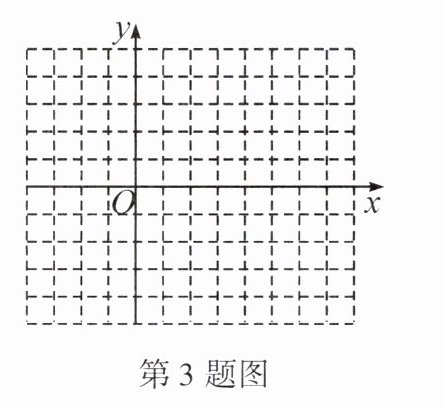
3. 如图,在平面直角坐标系中, $A, B$ 两点的坐标分别为 $(5,0)$、$(2,-4)$, 请你再找出一点 $C$, 使得以 $O, A, B, C$ 四点为顶点的四边形是菱形. 这时 $C$ 点的坐标为______.

答案： $(3,4)$或$(7,-4)$

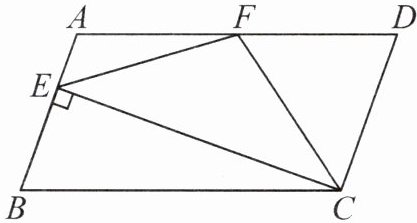
4. 如图,在 $\square A B C D$ 中, $A D= 2 A B, F$ 是 $A D$ 的中点, 作 $C E \perp A B$, 垂足 $E$ 在线段 $A B$ 上,连接 $E F, C F$, 则下列结论中一定成立的是______. (把所有正确结论的序号都填在横线上)
① $\angle D C F= \frac{1}{2} \angle B C D$; ② $E F= C F$; ③ $S_{\triangle B E C}= 2 S_{\triangle C E F}$; ④ $\angle D F E= 3 \angle A E F$.

答案： ①②④