《2025年快乐暑假天天练八年级数学》

3. 先化简,再求值:$(1-\frac {1}{m-2})÷\frac {m^{2}-6m+9}{m-2}$,其中$m= 5$.

答案： 【解析】：
本题可先对原式进行化简，再将$m = 5$代入化简后的式子求值。
- **步骤一：化简原式**
化简$1 - \frac{1}{m - 2}$：
对$1 - \frac{1}{m - 2}$进行通分，$1=\frac{m - 2}{m - 2}$，则$1 - \frac{1}{m - 2}=\frac{m - 2}{m - 2}-\frac{1}{m - 2}=\frac{m - 2 - 1}{m - 2}=\frac{m - 3}{m - 2}$。
化简$\frac{m^2 - 6m + 9}{m - 2}$：
根据完全平方公式$a^2-2ab+b^2=(a-b)^2$，对$m^2 - 6m + 9$进行因式分解，可得$m^2 - 6m + 9=(m - 3)^2$，则$\frac{m^2 - 6m + 9}{m - 2}=\frac{(m - 3)^2}{m - 2}$。
计算$(1 - \frac{1}{m - 2})÷\frac{m^2 - 6m + 9}{m - 2}$：
根据除法运算法则，除以一个数等于乘以它的倒数，则$(1 - \frac{1}{m - 2})÷\frac{m^2 - 6m + 9}{m - 2}=\frac{m - 3}{m - 2}\times\frac{m - 2}{(m - 3)^2}$，约分可得$\frac{1}{m - 3}$。
- **步骤二：代入求值**
将$m = 5$代入$\frac{1}{m - 3}$，可得$\frac{1}{5 - 3}=\frac{1}{2}$。
【答案】：$\frac{1}{2}$

4. 某商店决定购进A,B两种羽毛球拍进行销售,已知每副A种球拍的进价比每副B种球拍贵20元,用2800元购进A种球拍的数量与用2000元购进B种球拍的数量相同.
(1)求A,B两种羽毛球拍每副的进价;
(2)若该商店决定购进这两种羽毛球拍共100副,考虑市场需求和资金周转,用于购买这100副羽毛球拍的资金不超过5900元,那么该商店最多可购进A种羽毛球拍多少副?

答案： 【解析】：
### $(1)$求$A$，$B$两种羽毛球拍每副的进价
设$B$种羽毛球拍每副的进价为$x$元，因为每副$A$种球拍的进价比每副$B$种球拍贵$20$元，所以$A$种羽毛球拍每副的进价为$(x + 20)$元。
已知用$2800$元购进$A$种球拍的数量与用$2000$元购进$B$种球拍的数量相同，根据“数量$=$总价$\div$单价”，可列方程：
$\dfrac{2800}{x + 20}=\dfrac{2000}{x}$
交叉相乘得：$2800x = 2000(x + 20)$
去括号：$2800x = 2000x + 40000$
移项：$2800x - 2000x = 40000$
合并同类项：$800x = 40000$
解得：$x = 50$
把$x = 50$代入$x(x + 20)=50\times(50 + 20)=3500\neq0$，所以$x = 50$是原方程的解。
则$A$种羽毛球拍每副的进价为：$x + 20 = 50 + 20 = 70$（元）
### $(2)$求该商店最多可购进$A$种羽毛球拍的数量
设购进$A$种羽毛球拍$m$副，则购进$B$种羽毛球拍$(100 - m)$副。
已知$A$种羽毛球拍每副进价$70$元，$B$种羽毛球拍每副进价$50$元，且用于购买这$100$副羽毛球拍的资金不超过$5900$元，可列不等式：
$70m + 50(100 - m)\leq5900$
去括号：$70m + 5000 - 50m\leq5900$
移项：$70m - 50m\leq5900 - 5000$
合并同类项：$20m\leq900$
解得：$m\leq45$
【答案】：
$(1)$$A$种羽毛球拍每副进价$\boldsymbol{70}$元，$B$种羽毛球拍每副进价$\boldsymbol{50}$元；$(2)$该商店最多可购进$A$种羽毛球拍$\boldsymbol{45}$副。

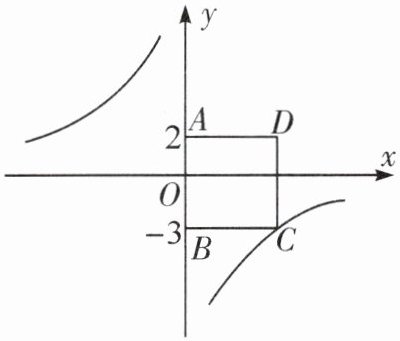
5. 如图,四边形ABCD为正方形.点A的坐标为$(0,2)$,点B的坐标为$(0,-3)$,反比例函数$y= \frac {k}{x}(k≠0)$的图象经过点C.
(1)点D的坐标为______;
(2)求反比例函数的解析式.

答案：
(1)$(5,2)$
(2)$y =-\frac{15}{x}$