《2025年快乐暑假天天练八年级数学》

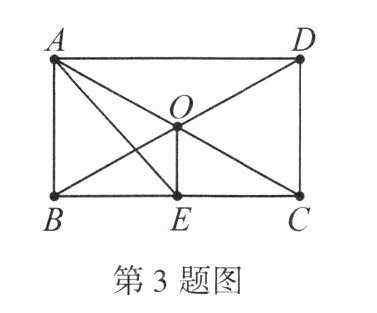
3. 如图,已知O是矩形ABCD对角线的交点,AE平分$∠BAD,∠AOD= 120^{\circ },∠AEO= $____.

答案： $30^{\circ}$

4. 如图,在正方形ABCD中,已知点E,F分别在BC,CD上,$△AEF$是等边三角形,连接AC交EF于G,给出下列结论:①$BE= DF$;②$∠DAF= 15^{\circ }$;③AC垂直平分EF;④$BE+DF= EF$.其中结论正确的有____.(只填序号)

答案： ①②③

1. 先化简,再求值:$(n-\frac {1}{n})÷\frac {n^{2}-2n+1}{n}$,其中,$n= -3.$

答案： 【解析】：
本题可先对原式进行化简，再将$n = - 3$代入化简后的式子求值。
- **步骤一：化简原式$(n - \frac{1}{n}) \div \frac{n^2 - 2n + 1}{n}$。**
化简括号内的式子：
对$n - \frac{1}{n}$进行通分，可得$\frac{n^2}{n} - \frac{1}{n}=\frac{n^2 - 1}{n}$。
对除法式子变形：
根据除法运算法则，除以一个数等于乘以它的倒数，则$(n - \frac{1}{n}) \div \frac{n^2 - 2n + 1}{n}=\frac{n^2 - 1}{n} \times \frac{n}{n^2 - 2n + 1}$。
对分子分母进行因式分解：
根据平方差公式$a^2-b^2=(a+b)(a-b)$，可得$n^2 - 1=(n + 1)(n - 1)$；
根据完全平方公式$a^2-2ab+b^2=(a-b)^2$，可得$n^2 - 2n + 1=(n - 1)^2$。
化简式子：
将因式分解后的式子代入$\frac{n^2 - 1}{n} \times \frac{n}{n^2 - 2n + 1}$，可得$\frac{(n + 1)(n - 1)}{n} \times \frac{n}{(n - 1)^2}$，约分后得到$\frac{n + 1}{n - 1}$。
- **步骤二：代入$n = - 3$求值。**
将$n = - 3$代入$\frac{n + 1}{n - 1}$，可得$\frac{-3 + 1}{-3 - 1}=\frac{-2}{-4}=\frac{1}{2}$。
【答案】：$\frac{1}{2}$

2. 若正比例函数$y= -2x的图象与一次函数y= x+m$的图象交于点A,且点A的横坐标为-3.
(1)求该一次函数的解析式;
(2)直接写出方程组$\left\{\begin{array}{l} y= -2x,\\ y= x+m\end{array}\right. $的解.

答案： 【解析】：1. 首先求点$A$的坐标：
已知正比例函数$y = - 2x$，点$A$在$y=-2x$上且横坐标为$-3$，把$x = - 3$代入$y=-2x$，可得$y=-2\times(-3)=6$，所以点$A$的坐标为$(-3,6)$。
2. 然后求一次函数的解析式：
因为点$A(-3,6)$在一次函数$y = x + m$的图象上，把$x=-3$，$y = 6$代入$y=x + m$中，得到$6=-3 + m$。
解方程$6=-3 + m$，移项可得$m=6 + 3=9$，所以一次函数的解析式为$y=x + 9$。
3. 最后求方程组的解：
方程组$\left\{\begin{array}{l}y=-2x\\y=x + m\end{array}\right.$的解就是两个函数图象交点的坐标。
已知两函数图象交点$A$的坐标为$(-3,6)$，所以方程组$\left\{\begin{array}{l}y=-2x\\y=x + 9\end{array}\right.$的解为$\left\{\begin{array}{l}x=-3\\y=6\end{array}\right.$。
【答案】：1. $y=x + 9$ 2. $\left\{\begin{array}{l}x=-3\\y=6\end{array}\right.$