《2025年快乐暑假天天练八年级数学》

2. 有5个数的平均数是8,另有15个数的平均数是20,那么这20个数的平均数是______.

答案： $17$

3. 已知反比例函数$y= \frac {k}{x}的图象经过点(2,4)$、$(m,n)$,则mn的值为______.

答案： $8$

4. 如图,已知矩形ABCD的对角线AC,BD相交于点O,$∠AOD= 120^{\circ },AB= 5cm$,则矩形对角线的长是______cm.

答案： 10

5. 如图,在平行四边形ABCD中,$AB= 3,∠ABC的平分线与∠BCD$的平分线交于点E,若点E恰好在边AD上,则$BE^{2}+CE^{2}$的值为______.

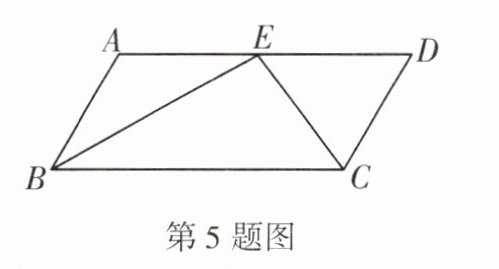
答案： $36$

1. 计算:$(\frac {1}{2})^{0}+|-\frac {1}{3}|-3^{-1}$.

答案： 【解析】：本题可根据零指数幂、绝对值和负整数指数幂的运算法则分别计算各项，再进行加减运算。
**步骤一：计算$(\frac{1}{2})^0$的值**
根据零指数幂的运算法则：任何非零数的$0$次幂都等于$1$，可得$(\frac{1}{2})^0 = 1$。
**步骤二：计算$\vert -\frac{1}{3}\vert$的值**
根据绝对值的性质：正数和$0$的绝对值是它本身，负数的绝对值是它的相反数，可得$\vert -\frac{1}{3}\vert = \frac{1}{3}$。
**步骤三：计算$3^{-1}$的值**
根据负整数指数幂的运算法则：$a^{-p}=\frac{1}{a^p}$（$a\neq0$，$p$为正整数），可得$3^{-1} = \frac{1}{3^1} = \frac{1}{3}$。
**步骤四：计算原式的值**
将上述计算结果代入原式可得：
$(\frac{1}{2})^0 + \vert -\frac{1}{3}\vert - 3^{-1} = 1 + \frac{1}{3} - \frac{1}{3} = 1$。
【答案】：$1$

2. 如图,已知AC是平行四边形ABCD的对角线,过点D作$DE⊥DC$,交AC于点E,过点B作$BF⊥AB$,交AC于点F.
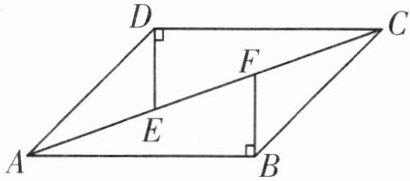
求证:$CE= AF$.

答案： 【解析】：
因为四边形$ABCD$是平行四边形，所以$AD = BC$，$AD// BC$，则$\angle DAE=\angle BCF$。
又因为$DE\perp DC$，$BF\perp AB$，$AB// DC$，所以$\angle EDC=\angle FBA = 90^{\circ}$，$\angle ADE=\angle CBF$。
在$\triangle ADE$和$\triangle CBF$中，$\begin{cases}\angle DAE=\angle BCF\\AD = BC\\\angle ADE=\angle CBF\end{cases}$，根据$ASA$（角边角）定理可得$\triangle ADE\cong\triangle CBF$。
所以$AE = CF$，因为$AE + EF=CF + EF$，所以$CE = AF$。
【答案】：
因为四边形$ABCD$是平行四边形，所以$AD = BC$，$AD// BC$，$\angle DAE=\angle BCF$。
又$DE\perp DC$，$BF\perp AB$，$AB// DC$，所以$\angle EDC=\angle FBA = 90^{\circ}$，$\angle ADE=\angle CBF$。
在$\triangle ADE$和$\triangle CBF$中，$\begin{cases}\angle DAE=\angle BCF\\AD = BC\\\angle ADE=\angle CBF\end{cases}$，$\triangle ADE\cong\triangle CBF(ASA)$。
所以$AE = CF$，则$AE + EF=CF + EF$，即$CE = AF$。