《2025年快乐暑假天天练八年级数学》

1. 若方程 $\frac{2kx + 5}{x + 2} = 1$ 的解为 $x = 1$,则 $k$ 的值为____.

答案： $-1$

2. 如图,点 $E$ 在正方形 $ABCD$ 的边 $AB$ 上,若 $EB = 1,EC = 2$,则正方形 $ABCD$ 的面积为____.

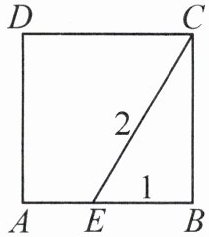
答案： $3$

3. 如图,一次函数 $y = mx$ 与反比例函数 $y = \frac{k}{x}$ 的图象交于 $A,B$ 两点,过点 $A$ 作 $AM \perp x$ 轴,垂足为 $M$,连接 $BM$,若 $S_{\triangle ABM} = 3$,则 $k$ 的值是____.

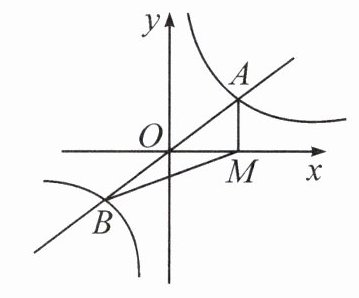
答案： $3$

4. 跳远运动员李刚对训练效果进行测试,6 次跳远的成绩(单位:m)如下:7.6,7.8,7.7,7.8,8.0,7.9. 这 6 次成绩的平均数为 7.8,方差为 $\frac{1}{60}$. 如果李刚再跳两次,成绩分别为 7.7,7.9,则李刚这 8 次跳远成绩的方差____(填“变大”“不变”或“变小”).

答案： 变小

1. 先化简分式 $(\frac{x}{x - 1} - \frac{x}{x - 2}) ÷ \frac{x^2 - x}{x^2 - 2x + 1}$,然后从 $-1 \leq x \leq 3$ 中选取一个你认为合适的整数 $x$ 代入求值.

答案： 【解析】：
1. 首先化简$(\frac{x}{x - 1}-\frac{x}{x - 2})\div\frac{x^{2}-x}{x^{2}-2x + 1}$：
先对括号内的式子进行通分，$\frac{x}{x - 1}-\frac{x}{x - 2}=\frac{x(x - 2)-x(x - 1)}{(x - 1)(x - 2)}$。
展开分子：$x(x - 2)-x(x - 1)=x^{2}-2x-(x^{2}-x)=x^{2}-2x - x^{2}+x=-x$。
所以$\frac{x}{x - 1}-\frac{x}{x - 2}=\frac{-x}{(x - 1)(x - 2)}$。
再看除法运算，根据除法运算法则$a\div b=a\times\frac{1}{b}$，$\frac{x^{2}-x}{x^{2}-2x + 1}=\frac{x(x - 1)}{(x - 1)^{2}}=\frac{x}{x - 1}$（$x\neq1$）。
则$(\frac{x}{x - 1}-\frac{x}{x - 2})\div\frac{x^{2}-x}{x^{2}-2x + 1}=\frac{-x}{(x - 1)(x - 2)}\times\frac{x - 1}{x}$。
约分可得$-\frac{1}{x - 2}$。
2. 然后确定$x$的取值：
要使原式有意义，则分母不能为$0$。
在$\frac{x}{x - 1}-\frac{x}{x - 2}$中，$x-1\neq0$且$x - 2\neq0$；在$\frac{x^{2}-x}{x^{2}-2x + 1}$中，$x\neq0$且$x - 1\neq0$。
即$x\neq0$，$x\neq1$，$x\neq2$。
已知$-1\leq x\leq3$，取整数$x = 3$。
3. 最后代入求值：
当$x = 3$时，$-\frac{1}{x - 2}=-\frac{1}{3 - 2}=-1$。
【答案】：化简结果为$-\frac{1}{x - 2}$，当$x = 3$时，值为$-1$。