《2025年快乐暑假天天练八年级数学》

1. 计算:$|-5|-2022^{0}+(\frac {1}{2})^{-1}= $____.

答案： $6$

2. 如图,在四边形$ABCD$中,$AB= BC= CD= DA$,对角线$AC与BD相交于点O$,若不增加任何字母与辅助线,要使四边形$ABCD$是正方形,则还需增加一个条件是____.

答案： $AC = BD$（答案不唯一，也可以是$\angle BAD = 90^{\circ}$等）

3. 已知关于$x的方程\frac {x+a}{x-2}= -1有解且大于0$,则$a$的取值范围是____.

答案： $a＜2$且$a\neq - 2$

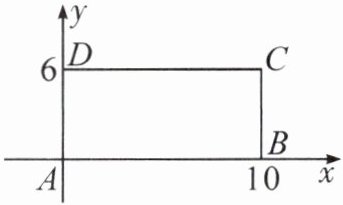
4. 如图,已知平面上四点$A(0,0),B(10,0),C(10,6),D(0,6)$,直线$y= mx-3m+2(m≠0)将四边形ABCD$分成面积相等的两部分,则$m$的值为____.

答案： $\boldsymbol{\frac{1}{2}}$

1. 先化简$(\frac {1}{x-1}-\frac {1}{x+1})÷\frac {x}{2x^{2}-2}$的值,然后选择一个你喜欢的$x$的值代入求原式的值.

答案： 【解析】：
1. 首先化简$(\frac{1}{x - 1}-\frac{1}{x + 1})\div\frac{x}{2x^{2}-2}$：
对括号内的式子进行通分，$\frac{1}{x - 1}-\frac{1}{x + 1}=\frac{x + 1-(x - 1)}{(x - 1)(x + 1)}$。
去括号得$\frac{x + 1 - x+1}{(x - 1)(x + 1)}=\frac{2}{(x - 1)(x + 1)}$。
对$2x^{2}-2$进行因式分解，$2x^{2}-2 = 2(x^{2}-1)=2(x - 1)(x + 1)$。
则原式变为$\frac{2}{(x - 1)(x + 1)}\div\frac{x}{2(x - 1)(x + 1)}$。
根据除法运算法则，除以一个数等于乘以它的倒数，即$\frac{2}{(x - 1)(x + 1)}\times\frac{2(x - 1)(x + 1)}{x}=\frac{4}{x}$。
2. 然后选择$x$的值代入：
因为原式分母不能为$0$，即$x-1\neq0$，$x + 1\neq0$，$x\neq0$，所以$x\neq\pm1$且$x\neq0$。
不妨取$x = 2$，代入$\frac{4}{x}$得$\frac{4}{2}=2$。
【答案】：化简结果为$\frac{4}{x}$，当$x = 2$时，原式的值为$2$。

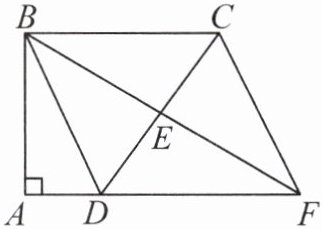
2. 如图,在四边形$ABCD$中,$∠A= ∠ABC= 90^{\circ }$,$E是边CD$的中点,连接$BE$并延长,求证:四边形$BDFC$是平行四边形.

答案： 【解析】：
已知$\angle A=\angle ABC = 90^{\circ}$，所以$BC// AF$（同旁内角互补，两直线平行）。
因为$E$是边$CD$的中点，所以$CE = DE$。
又因为$BC// AF$，所以$\angle BCE=\angle FDE$（两直线平行，内错角相等）。
在$\triangle BCE$和$\triangle FDE$中：
$\begin{cases}\angle BCE=\angle FDE\\CE = DE\\\angle BEC=\angle FED\end{cases}$（对顶角相等）
所以$\triangle BCE\cong\triangle FDE(ASA)$。
则$BE = FE$（全等三角形对应边相等）。
又因为$CE = DE$，所以四边形$BDFC$是平行四边形（对角线互相平分的四边形是平行四边形）。
【答案】：
因为$\angle A=\angle ABC = 90^{\circ}$，所以$BC// AF$，则$\angle BCE=\angle FDE$。
又$E$是$CD$中点，即$CE = DE$，且$\angle BEC=\angle FED$，所以$\triangle BCE\cong\triangle FDE(ASA)$，得$BE = FE$。
因为$CE = DE$，$BE = FE$，所以四边形$BDFC$是平行四边形（对角线互相平分的四边形是平行四边形）。