1. 一次函数 $ y = kx + 1 $ 的图象经过点 $ (1,2) $,反比例函数 $ y = \frac{k}{x} $ 的图象经过点 $ (m, \frac{1}{2}) $,则 $ m = $____.
答案:
1. $2$
2. 已知 $ P_1(x_1, y_1), P_2(x_2, y_2) $ 是同一个反比例函数图象上的两点,若 $ \frac{1}{x_2} = \frac{1}{x_1} + 2 $,且 $ y_2 = y_1 - \frac{1}{2} $,则这个反比例函数的表达式为____.
答案:
$y = -\frac{1}{4x}$
3. 直线 $ y_1 = k_1x + b_1(k_1 > 0) $ 与 $ y_2 = k_2x + b_2(k_2 < 0) $ 相交于点 $ (-2,0) $,且两直线与 $ y $ 轴围成的三角形面积为 4,那么 $ b_1 - b_2 $ 等于____.
答案:
$4$
4. 一个装有进水管和出水管的容器,从某时刻开始的 4 分钟内只进水不出水,在随后的 8 分钟内既进水又出水,接着关闭进水管直到容器内的水放完. 假设每分钟的进水量和出水量是两个常数,容器内的水量 $ y $ (单位:升) 与时间 $ x $ (单位:分) 之间的部分关系如图所示. 那么,从关闭进水管起____分钟该容器内的水恰好放完.
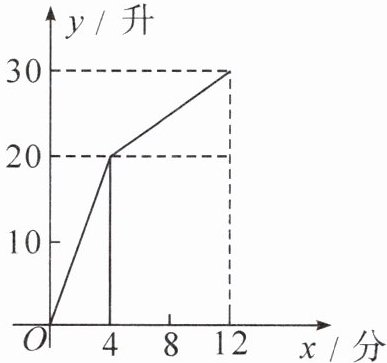

答案:
$8$
1. 一次函数图象经过 $ (3,1),(2,0) $ 两点.
(1) 求这个一次函数的解析式;
(2) 当 $ x = 6 $ 时,求 $ y $ 的值.
(1) 求这个一次函数的解析式;
(2) 当 $ x = 6 $ 时,求 $ y $ 的值.
答案:
【解析】:1. 设该一次函数的解析式为$y = kx + b$($k\neq0$)。
因为函数图象经过$(3,1)$,$(2,0)$两点,将这两点代入解析式可得方程组$\begin{cases}3k + b = 1\\2k + b = 0\end{cases}$。
用第一个方程$3k + b = 1$减去第二个方程$2k + b = 0$,可得:
$(3k + b)-(2k + b)=1 - 0$,去括号得$3k + b - 2k - b = 1$,合并同类项得$k = 1$。
把$k = 1$代入$2k + b = 0$,即$2\times1 + b = 0$,解得$b=-2$。
所以这个一次函数的解析式为$y = x - 2$。
2. 当$x = 6$时,把$x = 6$代入$y = x - 2$,可得$y=6 - 2 = 4$。
【答案】:1.$y = x - 2$ 2.$4$
因为函数图象经过$(3,1)$,$(2,0)$两点,将这两点代入解析式可得方程组$\begin{cases}3k + b = 1\\2k + b = 0\end{cases}$。
用第一个方程$3k + b = 1$减去第二个方程$2k + b = 0$,可得:
$(3k + b)-(2k + b)=1 - 0$,去括号得$3k + b - 2k - b = 1$,合并同类项得$k = 1$。
把$k = 1$代入$2k + b = 0$,即$2\times1 + b = 0$,解得$b=-2$。
所以这个一次函数的解析式为$y = x - 2$。
2. 当$x = 6$时,把$x = 6$代入$y = x - 2$,可得$y=6 - 2 = 4$。
【答案】:1.$y = x - 2$ 2.$4$
2. 如图,反比例函数的图象经过点 $ A,B $,点 $ A $ 的坐标为 $ (1,3) $,点 $ B $ 的纵坐标为 1,点 $ C $ 的坐标为 $ (2,0) $.
(1) 求该反比例函数的表达式;
(2) 求直线 $ BC $ 的表达式.
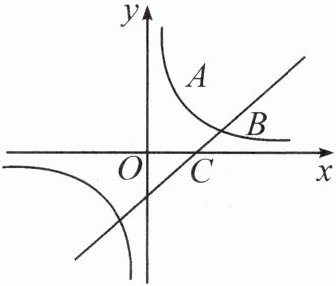
(1) 求该反比例函数的表达式;
(2) 求直线 $ BC $ 的表达式.

答案:
【解析】:
(1) 设反比例函数表达式为$y = \frac{k}{x}(k\neq0)$,因为反比例函数图象经过点$A(1,3)$,将$A(1,3)$代入$y = \frac{k}{x}$中,可得$3=\frac{k}{1}$,解得$k = 3$,所以该反比例函数的表达式为$y=\frac{3}{x}$。
(2) 因为点$B$在反比例函数$y=\frac{3}{x}$图象上,且点$B$纵坐标为$1$,把$y = 1$代入$y=\frac{3}{x}$,得$1=\frac{3}{x}$,解得$x = 3$,所以点$B$的坐标为$(3,1)$。
设直线$BC$的表达式为$y=mx + n(m\neq0)$,把$B(3,1)$,$C(2,0)$代入$y=mx + n$中,得到$\begin{cases}3m + n = 1\\2m + n = 0\end{cases}$,用$3m + n = 1$减去$2m + n = 0$,即$(3m + n)-(2m + n)=1 - 0$,$3m + n - 2m - n = 1$,解得$m = 1$。
把$m = 1$代入$2m + n = 0$,得$2\times1 + n = 0$,解得$n=-2$。
所以直线$BC$的表达式为$y=x - 2$。
【答案】:
(1)$y=\frac{3}{x}$
(2)$y=x - 2$
(1) 设反比例函数表达式为$y = \frac{k}{x}(k\neq0)$,因为反比例函数图象经过点$A(1,3)$,将$A(1,3)$代入$y = \frac{k}{x}$中,可得$3=\frac{k}{1}$,解得$k = 3$,所以该反比例函数的表达式为$y=\frac{3}{x}$。
(2) 因为点$B$在反比例函数$y=\frac{3}{x}$图象上,且点$B$纵坐标为$1$,把$y = 1$代入$y=\frac{3}{x}$,得$1=\frac{3}{x}$,解得$x = 3$,所以点$B$的坐标为$(3,1)$。
设直线$BC$的表达式为$y=mx + n(m\neq0)$,把$B(3,1)$,$C(2,0)$代入$y=mx + n$中,得到$\begin{cases}3m + n = 1\\2m + n = 0\end{cases}$,用$3m + n = 1$减去$2m + n = 0$,即$(3m + n)-(2m + n)=1 - 0$,$3m + n - 2m - n = 1$,解得$m = 1$。
把$m = 1$代入$2m + n = 0$,得$2\times1 + n = 0$,解得$n=-2$。
所以直线$BC$的表达式为$y=x - 2$。
【答案】:
(1)$y=\frac{3}{x}$
(2)$y=x - 2$
查看更多完整答案,请扫码查看


