21. (15分)有一个可自由转动的转盘,被分成了三个大小相同的扇形,分别标有数字2、4、6;另有一个不透明的瓶子,装有分别标有数字1、3、5的三个完全相同的小球(如图)。小杰先转动一次转盘,停止后记下指针指向的数字(若指针指在分界线上则重转),小玉再从瓶子中随机取出一个小球,记下小球上的数字。将小杰记下的数字用$a$表示,小玉记下的数字用$b$表示,这两个数字组成的数对用$(a,b)$表示。
(1)请用列表或画树状图的方法表示出所有数对$(a,b)$可能出现的结果。
(2)若得到的两个数字之和是3的倍数,则小杰赢;若得到的两个数字之和是7的倍数,则小玉赢。此游戏公平吗?为什么?
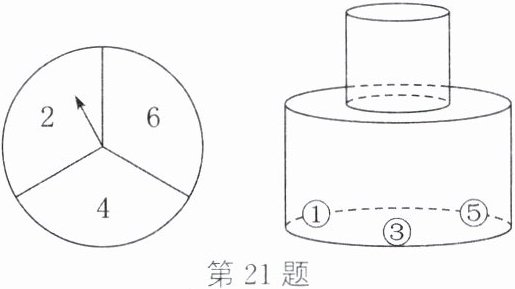
(1)请用列表或画树状图的方法表示出所有数对$(a,b)$可能出现的结果。
(2)若得到的两个数字之和是3的倍数,则小杰赢;若得到的两个数字之和是7的倍数,则小玉赢。此游戏公平吗?为什么?

答案:
(1) 列表如下:
| 转盘 $a$ \ 小球 $b$ | 1 | 3 | 5 |
|----------------------|-----|-----|-----|
| 2 | (2,1)| (2,3)| (2,5)|
| 4 | (4,1)| (4,3)| (4,5)|
| 6 | (6,1)| (6,3)| (6,5)|
所有可能结果:$(2,1)$,$(2,3)$,$(2,5)$,$(4,1)$,$(4,3)$,$(4,5)$,$(6,1)$,$(6,3)$,$(6,5)$。
(2) 此游戏公平。
理由如下:
由(1)可知,一共有9种等可能结果,其中和是3的倍数有3种,和是7的倍数有3种。
$P(小杰赢)=\frac{3}{9}=\frac{1}{3}$,
$P(小玉赢)=\frac{3}{9}=\frac{1}{3}$,
$\because P(小杰赢)=P(小玉赢)$,
$\therefore$ 此游戏公平。
| 转盘 $a$ \ 小球 $b$ | 1 | 3 | 5 |
|----------------------|-----|-----|-----|
| 2 | (2,1)| (2,3)| (2,5)|
| 4 | (4,1)| (4,3)| (4,5)|
| 6 | (6,1)| (6,3)| (6,5)|
所有可能结果:$(2,1)$,$(2,3)$,$(2,5)$,$(4,1)$,$(4,3)$,$(4,5)$,$(6,1)$,$(6,3)$,$(6,5)$。
(2) 此游戏公平。
理由如下:
由(1)可知,一共有9种等可能结果,其中和是3的倍数有3种,和是7的倍数有3种。
$P(小杰赢)=\frac{3}{9}=\frac{1}{3}$,
$P(小玉赢)=\frac{3}{9}=\frac{1}{3}$,
$\because P(小杰赢)=P(小玉赢)$,
$\therefore$ 此游戏公平。
查看更多完整答案,请扫码查看


