《2025年通成学典课时作业本九年级数学上册苏科版苏州专版》

18. （5分）如图，四边形$ABCD$内接于$\odot O$，$∠C=2∠A$，$DE$是$\odot O$的直径，连接$BD$、$BE$.
（1）求$∠A$的度数；
（2）若$\odot O$的直径为4，求$BE$的长.

答案： （1）
∵四边形$ABCD$内接于$\odot O$，$\therefore \angle A + \angle C = 180°$。
又$\angle C = 2\angle A$，设$\angle A = x$，则$x + 2x = 180°$，解得$x = 60°$。
$\therefore \angle A = 60°$。
（2）$\because DE$是$\odot O$的直径，直径为$4$，$\therefore DE = 4$，且$\angle DBE = 90°$（直径所对圆周角为直角）。
$\angle C = 2\angle A = 120°$，$\angle C$为圆周角，所对优弧$BD$，$\therefore$优弧$BD$度数为$2\angle C = 240°$。
$\therefore$劣弧$BD$度数为$360° - 240° = 120°$。
$\angle BED$为劣弧$BD$所对圆周角，$\therefore \angle BED = \frac{1}{2} × 120° = 60°$。
在$Rt\triangle DBE$中，$\cos\angle BED = \frac{BE}{DE}$，$\therefore BE = DE \cdot \cos60° = 4 × \frac{1}{2} = 2$。
（1）$60°$；（2）$2$。

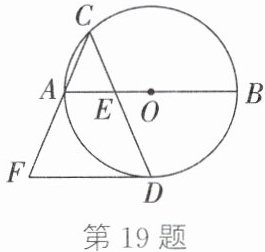
19. （6分）如图，$AB$是$\odot O$的直径，$FD$为$\odot O$的切线，弦$CD$与$AB$相交于点$E$，$DF// AB$，交$CA$的延长线于点$F$，$CF=CD$，求$∠F$的度数.

答案： 45°

20. （6分）如图是某香水瓶示意图，它可以近似看成$\odot O$割去两个弓形后余下的部分与矩形$ABCD$组合而成的图形（点$B$、$C$在$\odot O$上），其中$BC// EF$，已知$\odot O$的半径为2.5cm，$BC=1.4cm$，$AB=2.6cm$，$EF=4.8cm$，求香水瓶的高度$h$.

答案： 连接OB、OC，过点O作OH⊥BC于点H，垂足为H，延长HO交EF于点G。
∵BC=1.4cm，OH⊥BC，
∴BH=BC/2=0.7cm。
在Rt△OBH中，OB=2.5cm，BH=0.7cm，
由勾股定理得：OH=√(OB²-BH²)=√(2.5²-0.7²)=√(6.25-0.49)=√5.76=2.4cm。
同理，过点O作OG⊥EF于点G，EF=4.8cm，
∴EG=EF/2=2.4cm。
在Rt△OEG中，OE=2.5cm，EG=2.4cm，
由勾股定理得：OG=√(OE²-EG²)=√(2.5²-2.4²)=√(6.25-5.76)=√0.49=0.7cm。
∵BC//EF，
∴H、O、G三点共线，HG=OH+OG=2.4+0.7=3.1cm。
香水瓶高度h=HG+AB=3.1+2.6=5.7cm。
答：香水瓶的高度h为5.7cm。