《2025年通成学典课时作业本九年级数学上册苏科版苏州专版》

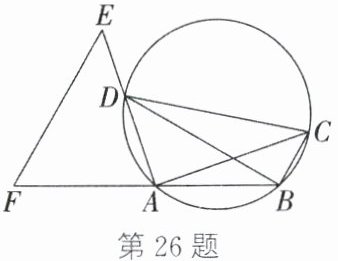
26. （10分）如图，在圆内接四边形$ABCD$中，$AD ＜ AC$，$\angle ADC ＜ \angle BAD$，延长$AD$至点$E$，使$AE = AC$，延长$BA$至点$F$，连接$EF$，使$\angle AFE=\angle ADC$。
（1）若$\angle AFE = 60^{\circ}$，$CD$为直径，求$\angle ABD$的度数。
（2）求证：
① $EF// BC$；
② $EF = BD$。

答案： （1）30°；（2）①见解析；②见解析

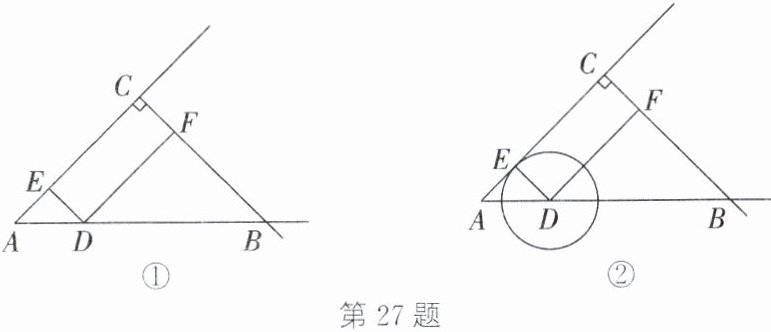
27. （10分）如图①，在$\mathrm{Rt}\triangle ABC$中，$\angle ACB = 90^{\circ}$，$AC = BC$，$AB = 10\mathrm{cm}$，点$D$从点$A$出发，沿射线$AB$以$2\mathrm{cm/s}$的速度移动，移动过程中始终保持$DE// BC$，$DF// AC$（点$E$、$F$分别在射线$AC$、$CB$上）。设点$D$移动的时间为$t\mathrm{s}$。
（1）若点$D$在边$AB$上，则当$t$为何值时，四边形$DFCE$的面积为$12\mathrm{cm}^{2}$？
（2）如图②，以点$D$为圆心，$DE$为半径作$\odot D$。在点$D$沿射线$AB$移动的过程中，是否存在$t$的值，使$\odot D$正好经过点$B$？若存在，请求出$t$的值；若不存在，请说明理由。

答案： （1）t=2或3；（2）存在，t=10-5√2或10+5√2。