《2025年通成学典课时作业本九年级数学上册苏科版苏州专版》

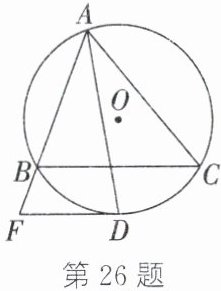
26. (10分)如图，$\odot O$的半径为5，$B$、$C$是$\odot O$上两定点，$A$是$\odot O$上一动点，且$∠BAC=60^{\circ}$，$∠BAC$的平分线交$\odot O$于点$D$.
(1)求证：$D$为$\overset{\frown}{BC}$上一定点.
(2)过点$D$作$BC$的平行线，交$AB$的延长线于点$F$.
① 判断$DF$与$\odot O$的位置关系，并说明理由；
② 若$\triangle ABC$为锐角三角形，则$DF$长的取值范围是.

答案：
(1) 连接OB、OC、OD。
∵∠BAC=60°，AD平分∠BAC，
∴∠BAD=∠CAD=30°。
∵B、C为定点，
∴弧BC为定弧，∠BAC=60°对应弧BC度数为120°。AD平分∠BAC，
∴弧BD=弧CD=60°，故D为弧BC中点，即D为定点。
(2) ① DF与⊙O相切。理由：连接OD，由
(1)知D为弧BC中点，
∴OD⊥BC（垂径定理）。
∵DF//BC，
∴OD⊥DF。
∵OD为半径，
∴DF是⊙O切线。
② (5√3,10]

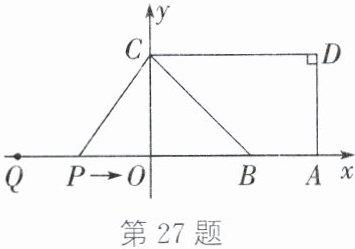
27. (10分)如图，点$A$的坐标为$(5,0)$，点$B$的坐标为$(3,0)$，点$C$在$y$轴的正半轴上，$∠CBO=45^{\circ}$，$CD// AB$，$∠CDA=90^{\circ}$. 点$P$从点$Q(-4,0)$出发，沿$x$轴向右以每秒2个单位长度的速度运动，运动时间为$t$秒.
(1)求点$C$的坐标.
(2)当点$P$在点$B$的左侧，且$∠BCP=15^{\circ}$时，求$t$的值.
(3)以点$P$为圆心、$PC$为半径的$\odot P$随点$P$的运动而变化. 若$\odot P$与四边形$ABCD$的边(或边所在的直线)相切，则$t$的值为.
：课时

答案：
(1)(0,3)
(2)(4+√3)/2
(3)1/2，2，14/5