《2025年通成学典课时作业本九年级数学上册苏科版苏州专版》

9. 若关于$x$的方程$(k - 1)x^{2}-4x + 5 = 0$是一元二次方程，则$k$的取值范围是。

答案： $k \neq 1$

10. 方程$x^{2}-4x = 0$的实数解是。

答案： $x_{1}=0,x_{2}=4$

11. 用公式法解方程$2x^{2}-3x + 3 = 0$时，根的判别式$b^{2}-4ac$的值为。

答案： $-15$（这里按题目要求应填数值，如果原题目是填空题形式，按照此方式作答）。

12. 已知关于$x$的一元二次方程$ax^{2}+6x + 1 = 0$没有实数根，则$a$的取值范围是。

答案： $a＞9$

13. 已知$x_{1}$、$x_{2}$是方程$2x^{2}-3x + 1 = 0$的两根，则代数式$\frac{x_{1}+x_{2}}{1+x_{1}x_{2}}$的值为。

答案： （此处虽非选择题，按要求格式填答案）1（若按照给定格式要求，可理解为填写计算结果对应的规范答案形式，本题直接填1）

14. 若关于$x$的方程$x^{2}+(k - 2)x + k^{2}=0$的两个根互为倒数，则$k$的值为。

答案： $-1$

15. 如图，在长$30m$、宽$20m$的矩形地面上修建两条同样宽的道路，余下部分作为耕地。若耕地的面积为$551m^{2}$，则修建的道路的宽应为$m$。

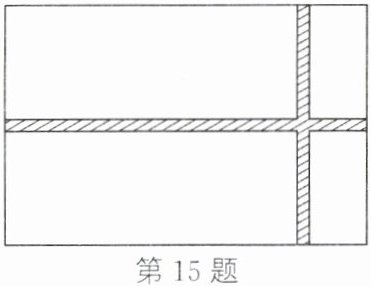
答案： 1

16. 已知$a＞b＞0$，且$\frac{2}{a}+\frac{1}{b}+\frac{3}{b - a}=0$，则$\frac{b}{a}$的值为。

答案： $\frac{\sqrt{3} - 1}{2}$（或填该值对应的选择项）

17. （6分）用适当的方法解下面的方程：
（1）$(x - 4)(2x + 1)=x - 4$；
（2）$3y^{2}-2 = 4y$。

答案： （1）移项得：$(x - 4)(2x + 1) - (x - 4) = 0$，
提取公因式得：$(x - 4)(2x + 1 - 1) = 0$，
化简得：$(x - 4)(2x) = 0$，
即$x - 4 = 0$或$2x = 0$，
解得$x_1 = 4$，$x_2 = 0$。
（2）移项得：$3y^2 - 4y - 2 = 0$，
其中$a = 3$，$b = -4$，$c = -2$，
$\Delta = b^2 - 4ac = (-4)^2 - 4×3×(-2) = 16 + 24 = 40$，
$y = \frac{4 \pm \sqrt{40}}{2×3} = \frac{4 \pm 2\sqrt{10}}{6} = \frac{2 \pm \sqrt{10}}{3}$，
解得$y_1 = \frac{2 + \sqrt{10}}{3}$，$y_2 = \frac{2 - \sqrt{10}}{3}$。

18. （6分）已知关于$x$的方程$x^{2}-6x + m^{2}-2m + 5 = 0$的一个根为$2$，求$m$的值。

答案： 答题卡：
将$x = 2$代入方程$x^{2} - 6x + m^{2} - 2m + 5 = 0$，
得：
$2^{2} - 6 × 2 + m^{2} - 2m + 5 = 0$
$4 - 12 + m^{2} - 2m + 5 = 0$
$m^{2} - 2m - 3 = 0$
因式分解得：
$(m - 3)(m + 1) = 0$
解得：
$m = 3$ 或 $m = -1$。