24. (8分)某种产品按质量分为$10$个档次,最低档次的产品每件可获得利润$24$元,每提高一个档次,每件产品的利润增加$2$元,最低档次的产品每天可生产$60$件,每提高一个档次,日产量将减少$2$件,并且每天只生产同一档次的产品(最低档次为第$1$档次,档次依次随质量的提高而提高)。
(1)某天生产第$3$档次的产品,求该档次每件产品的利润以及这一天的总利润;
(2)如果要使一天获得利润$1728$元,那么应生产第几档次的产品?
(1)某天生产第$3$档次的产品,求该档次每件产品的利润以及这一天的总利润;
(2)如果要使一天获得利润$1728$元,那么应生产第几档次的产品?
答案:
(1)
第3档次,相对于最低档次提高$3 - 1 = 2$个档次。
每件产品的利润:$24 + 2 × (3 - 1) = 24 + 4 = 28$(元)。
每天的生产量:$60 - 2 × (3 - 1) = 60 - 4 = 56$(件)。
一天的总利润:$28 × 56 = 1568$(元)。
所以该档次每件产品利润为28元,一天总利润为1568元。
(2)
设生产第$x$档次的产品。
每件产品的利润:$24 + 2(x - 1)$。
每天的生产量:$60 - 2(x - 1)$。
一天的总利润:$[24 + 2(x - 1)] × [60 - 2(x - 1)]$。
根据题意,建立方程:
$[24 + 2(x - 1)] × [60 - 2(x - 1)] = 1728$,
$(22 + 2x) × (62 - 2x) = 1728$(将x-1看作一个整体进行简化),
$1364+80x-4x^2= 1728$,
$4x^2-80x+364=0$,
$x^2 - 20x + 91 = 0$。
通过求解这个一元二次方程,得到:
$x_{1} = 7$,
$x_{2} = 13$(由于档次最高为10,所以$x_{2} = 13$不符合题意,舍去)。
所以应生产第7档次的产品。
第3档次,相对于最低档次提高$3 - 1 = 2$个档次。
每件产品的利润:$24 + 2 × (3 - 1) = 24 + 4 = 28$(元)。
每天的生产量:$60 - 2 × (3 - 1) = 60 - 4 = 56$(件)。
一天的总利润:$28 × 56 = 1568$(元)。
所以该档次每件产品利润为28元,一天总利润为1568元。
(2)
设生产第$x$档次的产品。
每件产品的利润:$24 + 2(x - 1)$。
每天的生产量:$60 - 2(x - 1)$。
一天的总利润:$[24 + 2(x - 1)] × [60 - 2(x - 1)]$。
根据题意,建立方程:
$[24 + 2(x - 1)] × [60 - 2(x - 1)] = 1728$,
$(22 + 2x) × (62 - 2x) = 1728$(将x-1看作一个整体进行简化),
$1364+80x-4x^2= 1728$,
$4x^2-80x+364=0$,
$x^2 - 20x + 91 = 0$。
通过求解这个一元二次方程,得到:
$x_{1} = 7$,
$x_{2} = 13$(由于档次最高为10,所以$x_{2} = 13$不符合题意,舍去)。
所以应生产第7档次的产品。
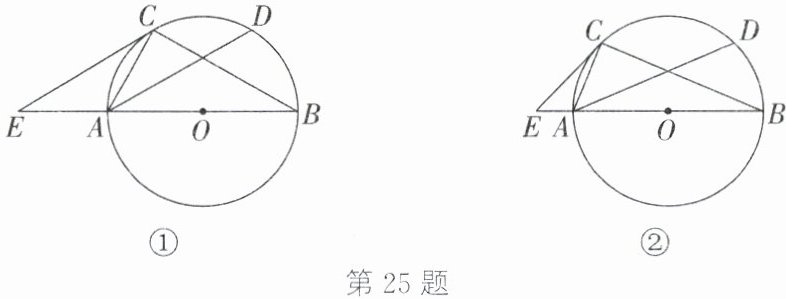
25. (8分)如图,$\odot O$是$\triangle ABC$的外接圆,$AB$是$\odot O$的直径,点$D$在$\overset{\frown}{BC}$上,$\overset{\frown}{AC}=\overset{\frown}{BD}$,点$E$在$BA$的延长线上,$\angle CEA=\angle CAD$。
(1)如图①,求证:$CE$是$\odot O$的切线;
(2)如图②,若$\angle CEA = 2\angle DAB$,$OA = 8$,则$\overset{\frown}{BD}$的长为。
(1)如图①,求证:$CE$是$\odot O$的切线;
(2)如图②,若$\angle CEA = 2\angle DAB$,$OA = 8$,则$\overset{\frown}{BD}$的长为。

答案:
(1)
证明:
连接$OC$,
因为$AB$是$\odot O$的直径,
所以$\angle ACB = 90^{\circ}$,
即$\angle CAD + \angle ABC=90^{\circ}$,
因为$OA = OC$,
所以$\angle CAO = \angle ACO$,
因为$\overset{\frown}{AC}=\overset{\frown}{BD}$,
所以$\angle ABC=\angle DAB=\angle ACO$,
因为$\angle CEA=\angle CAD$,
所以$\angle CEA+\angle ACO = \angle CAD+\angle ABC = 90^{\circ}$,
即$\angle ECO = 90^{\circ}$,
所以$OC\perp CE$,
又因为$OC$是$\odot O$的半径,
所以$CE$是$\odot O$的切线。
(2)
由(1)知$\angle ABC=\angle DAB$,
因为$\angle CEA = 2\angle DAB$,
设$\angle DAB = \alpha$,则$\angle CEA = 2\alpha$,
$\angle ABC=\angle DAB=\alpha$,
因为$\angle CEA=\angle CAD$,
所以$\angle CAD = 2\alpha$,
在$\triangle ABC$中,$\angle CAB=\angle CAD + \angle DAB=3\alpha$,
$\angle ABC=\alpha$,$\angle ACB = 90^{\circ}$,
根据三角形内角和为$180^{\circ}$,
可得$3\alpha+\alpha + 90^{\circ}=180^{\circ}$,
$4\alpha=90^{\circ}$,
解得$\alpha = 22.5^{\circ}$,
所以$\overset{\frown}{BD}$所对圆心角$\angle BOD = 2\angle DAB = 2\alpha=45^{\circ}$,
已知$OA = 8$,则$\odot O$半径$r = 8$,
根据弧长公式$l=\frac{n\pi r}{180}$(其中$n$为圆心角度数,$r$为半径),
可得$\overset{\frown}{BD}$的长为$\frac{45\pi×8}{180}=2\pi$。
故答案为$2\pi$。
(1)
证明:
连接$OC$,
因为$AB$是$\odot O$的直径,
所以$\angle ACB = 90^{\circ}$,
即$\angle CAD + \angle ABC=90^{\circ}$,
因为$OA = OC$,
所以$\angle CAO = \angle ACO$,
因为$\overset{\frown}{AC}=\overset{\frown}{BD}$,
所以$\angle ABC=\angle DAB=\angle ACO$,
因为$\angle CEA=\angle CAD$,
所以$\angle CEA+\angle ACO = \angle CAD+\angle ABC = 90^{\circ}$,
即$\angle ECO = 90^{\circ}$,
所以$OC\perp CE$,
又因为$OC$是$\odot O$的半径,
所以$CE$是$\odot O$的切线。
(2)
由(1)知$\angle ABC=\angle DAB$,
因为$\angle CEA = 2\angle DAB$,
设$\angle DAB = \alpha$,则$\angle CEA = 2\alpha$,
$\angle ABC=\angle DAB=\alpha$,
因为$\angle CEA=\angle CAD$,
所以$\angle CAD = 2\alpha$,
在$\triangle ABC$中,$\angle CAB=\angle CAD + \angle DAB=3\alpha$,
$\angle ABC=\alpha$,$\angle ACB = 90^{\circ}$,
根据三角形内角和为$180^{\circ}$,
可得$3\alpha+\alpha + 90^{\circ}=180^{\circ}$,
$4\alpha=90^{\circ}$,
解得$\alpha = 22.5^{\circ}$,
所以$\overset{\frown}{BD}$所对圆心角$\angle BOD = 2\angle DAB = 2\alpha=45^{\circ}$,
已知$OA = 8$,则$\odot O$半径$r = 8$,
根据弧长公式$l=\frac{n\pi r}{180}$(其中$n$为圆心角度数,$r$为半径),
可得$\overset{\frown}{BD}$的长为$\frac{45\pi×8}{180}=2\pi$。
故答案为$2\pi$。
查看更多完整答案,请扫码查看


