1. 利用公式法解得方程$3x^{2}-11x - 1 = 0$的两解分别为$a$、$b$,且$a > b$,则$a$的值为()
A.$\frac{-11+\sqrt{109}}{6}$
B.$\frac{-11+\sqrt{133}}{6}$
C.$\frac{11+\sqrt{109}}{6}$
D.$\frac{11+\sqrt{133}}{6}$
A.$\frac{-11+\sqrt{109}}{6}$
B.$\frac{-11+\sqrt{133}}{6}$
C.$\frac{11+\sqrt{109}}{6}$
D.$\frac{11+\sqrt{133}}{6}$
答案:
D
2. 下列圆的内接正多边形中,一条边所对的圆心角最大的图形是()
A.正三角形
B.正方形
C.正五边形
D.正六边形
A.正三角形
B.正方形
C.正五边形
D.正六边形
答案:
A
3. 已知关于$x$的方程$x^{2}-(2k - 2)x + k^{2}-1 = 0$有两个实数根,则实数$k$的取值范围是()
A.$k < 1$
B.$k\leqslant1$
C.$k > 1$
D.$k\geqslant1$
A.$k < 1$
B.$k\leqslant1$
C.$k > 1$
D.$k\geqslant1$
答案:
B
4. 如图,$AB$是$\odot O$的直径,$\angle E = 35^{\circ}$,则$\angle BOD$的度数为()
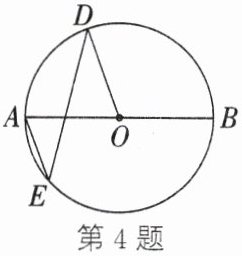
A.$80^{\circ}$
B.$100^{\circ}$
C.$120^{\circ}$
D.$110^{\circ}$

A.$80^{\circ}$
B.$100^{\circ}$
C.$120^{\circ}$
D.$110^{\circ}$
答案:
D
5. 已知$a$和$b$是方程$x^{2}+2024x - 4 = 0$的两个实数根,则$a^{2}+2023a - b$的值为()
A.$2025$
B.$2026$
C.$2027$
D.$2028$
A.$2025$
B.$2026$
C.$2027$
D.$2028$
答案:
D
6. 如图,$AB$是$\odot O$的切线,$A$为切点,连接$OA$,点$C$在$\odot O$上,$OC\perp OA$,连接$BC$并延长,交$\odot O$于点$D$,连接$OD$。若$\angle B = 65^{\circ}$,则$\angle DOC$的度数为()
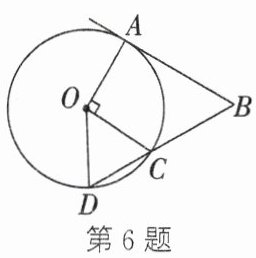
A.$45^{\circ}$
B.$50^{\circ}$
C.$65^{\circ}$
D.$75^{\circ}$

A.$45^{\circ}$
B.$50^{\circ}$
C.$65^{\circ}$
D.$75^{\circ}$
答案:
B
7. 如图,将$\triangle ABC$绕点$C$按顺时针方向旋转$120^{\circ}$得到$\triangle A'B'C$。已知$AC = 3$,$BC = 2$,则线段$AB$扫过的图形(涂色部分)的面积为()
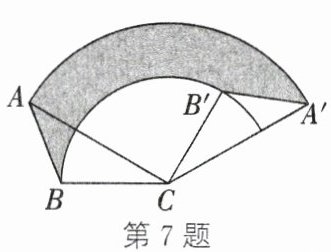
A.$\frac{5\pi}{3}$
B.$2\pi$
C.$\frac{5}{3}$
D.$2$

A.$\frac{5\pi}{3}$
B.$2\pi$
C.$\frac{5}{3}$
D.$2$
答案:
A
8. 如图,在边长为$2$的正六边形$ABCDEF$中,连接$BE$,点$H$在$BE$上运动,$G$为$EF$的中点。当$\triangle AGH$的周长最小时,$AH + GH$的长为()
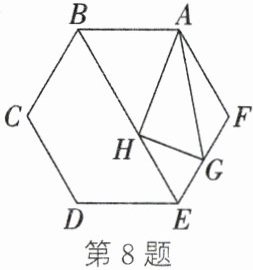
A.$2\sqrt{3}$
B.$\sqrt{13}$
C.$12$
D.$13$

A.$2\sqrt{3}$
B.$\sqrt{13}$
C.$12$
D.$13$
答案:
B
9. 方程$2x^{2}-7x = 0$的根为。
答案:
$0$或$\frac{7}{2}$(或 $x_{1}=0,x_{2}=\frac{7}{2}$ )
10. 已知关于$x$的方程$x^{2}+mx - 20 = 0$的一个根是$-4$,则它的另一个根是。
答案:
$5$
查看更多完整答案,请扫码查看


