《2025年通成学典课时作业本九年级数学上册苏科版苏州专版》

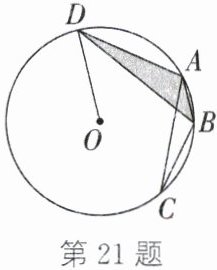
21. （6分）如图，$A$、$B$、$C$是$\odot O$上的点，连接$AB$、$AC$、$BC$，且$∠ACB=15^{\circ}$，过点$O$作$OD// AB$，交$\odot O$于点$D$，连接$AD$、$BD$. 若$\odot O$的半径为2，求图中涂色部分的面积.

答案： 连接OA、OB，
∵∠ACB=15°，∠ACB为圆周角，
∴弧AB的度数=2∠ACB=30°，
∴圆心角∠AOB=30°。
∵OA=OB=2，
∴△OAB的面积=1/2·OA·OB·sin∠AOB=1/2×2×2×sin30°=1/2×4×1/2=1。
∵OD//AB，
∴点D与点O到AB的距离相等（平行线间距离处处相等），
∴△ABD与△ABO同底AB，等高，
∴S_△ABD=S_△ABO=1。
答：图中涂色部分的面积为1。

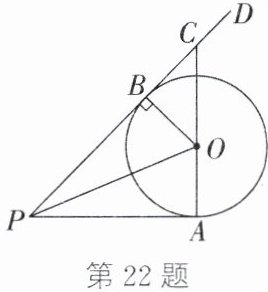
22. (8分)如图，$PO$平分$∠APD$，$PA$与$\odot O$相切于点$A$，延长$AO$，交$PD$于点$C$，过点$O$作$OB⊥PD$，垂足为$B$.
(1)求证：$PB$是$\odot O$的切线；
(2)若$\odot O$的半径为4，$OC=5$，则$PA$的长为.

答案：
(1) 证明：
∵PA与⊙O相切于点A，
∴OA⊥PA。
∵PO平分∠APD，OB⊥PD，OA⊥PA，
∴OA=OB（角平分线性质）。
∵OA为⊙O半径，
∴OB为⊙O半径。
∵OB⊥PD，
∴PB是⊙O的切线。
(2) 12
解析：
(2)
∵⊙O半径为4，
∴OA=OB=4。
在Rt△OBC中，OC=5，OB=4，
∴BC=√(OC²-OB²)=√(5²-4²)=3。
∵PA、PB为⊙O切线，
∴PA=PB（切线长定理）。设PA=PB=x，PC=y。
∵P、B、C共线，
∴PC=PB+BC=x+3。
在Rt△PAC中，AC=OA+OC=4+5=9，∠PAC=90°，
∴PA²+AC²=PC²，即x²+9²=(x+3)²。
解得x=12，即PA=12。

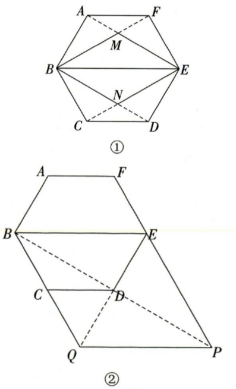
23. （8分）已知正六边形$ABCDEF$，请仅用无刻度的直尺完成下面的作图（保留作图痕迹，不写作法，用虚线表示作图过程，实线表示作图结果）.
（1）在图①中作出以$BE$为对角线的一个菱形$BMEN$；
（2）在图②中作出以$BE$为边的一个菱形$BEPQ$.

答案：