21. (6分)如图,在$\odot O$中,$C$是弦$AB$上的一个动点,连接$OC$,过点$C$作$CD\perp OC$,交$\odot O$于点$D$。
(1)当点$C$在$AB$的什么位置时,$CD$的长取得最大值?
(2)若$AB = 1$,求$CD$长的最大值。
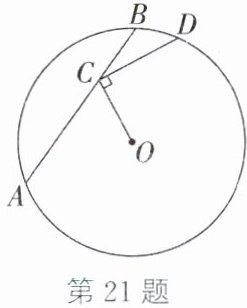
(1)当点$C$在$AB$的什么位置时,$CD$的长取得最大值?
(2)若$AB = 1$,求$CD$长的最大值。

答案:
(1)在Rt△OCD中,OD为⊙O半径(设为r),由勾股定理得:$CD=\sqrt{OD^2-OC^2}=\sqrt{r^2-OC^2}$。要使CD最大,需OC最小。圆心O到弦AB上点C的距离中,最短距离为O到AB的垂线段长,此时C为AB中点。故当点C是AB中点时,CD长取得最大值。
(2)设AB中点为M,由垂径定理得$AM=\frac{AB}{2}=\frac{1}{2}$,OM⊥AB。设OM=d,半径为r,在Rt△OAM中,$r^2=d^2+(\frac{1}{2})^2$。CD最大值时,$CD=\sqrt{r^2-d^2}=\sqrt{d^2+\frac{1}{4}-d^2}=\frac{1}{2}$。
(1)点C是AB的中点;(2)$\frac{1}{2}$
(2)设AB中点为M,由垂径定理得$AM=\frac{AB}{2}=\frac{1}{2}$,OM⊥AB。设OM=d,半径为r,在Rt△OAM中,$r^2=d^2+(\frac{1}{2})^2$。CD最大值时,$CD=\sqrt{r^2-d^2}=\sqrt{d^2+\frac{1}{4}-d^2}=\frac{1}{2}$。
(1)点C是AB的中点;(2)$\frac{1}{2}$
22. (8分)已知关于$x$的一元二次方程$x^{2}-(2m + 1)x + m^{2}+m = 0$。
(1)求证:无论$m$取何值,方程都有两个不相等的实数根。
(2)设该方程的两个实数根分别为$a$、$b$。若$(2a + b)(a + 2b)=20$,求$m$的值。
(1)求证:无论$m$取何值,方程都有两个不相等的实数根。
(2)设该方程的两个实数根分别为$a$、$b$。若$(2a + b)(a + 2b)=20$,求$m$的值。
答案:
(1)证明:对于方程$x^{2}-(2m + 1)x + m^{2}+m = 0$,判别式$\Delta = [-(2m+1)]^{2}-4×1×(m^{2}+m)$
$=4m^{2}+4m+1-4m^{2}-4m=1$
$\because\Delta=1>0$,$\therefore$无论$m$取何值,方程都有两个不相等的实数根。
(2)由韦达定理得:$a+b=2m+1$,$ab=m^{2}+m$
$\because(2a + b)(a + 2b)=2a^{2}+5ab+2b^{2}=2(a^{2}+b^{2})+5ab=2[(a+b)^{2}-2ab]+5ab=2(a+b)^{2}+ab$
$\therefore2(a+b)^{2}+ab=20$
将$a+b=2m+1$,$ab=m^{2}+m$代入得:
$2(2m+1)^{2}+(m^{2}+m)=20$
整理得:$2(4m^{2}+4m+1)+m^{2}+m=20$
$8m^{2}+8m+2+m^{2}+m-20=0$
$9m^{2}+9m-18=0$
即$m^{2}+m-2=0$
解得$m_{1}=-2$,$m_{2}=1$
$\therefore m$的值为$-2$或$1$。
$=4m^{2}+4m+1-4m^{2}-4m=1$
$\because\Delta=1>0$,$\therefore$无论$m$取何值,方程都有两个不相等的实数根。
(2)由韦达定理得:$a+b=2m+1$,$ab=m^{2}+m$
$\because(2a + b)(a + 2b)=2a^{2}+5ab+2b^{2}=2(a^{2}+b^{2})+5ab=2[(a+b)^{2}-2ab]+5ab=2(a+b)^{2}+ab$
$\therefore2(a+b)^{2}+ab=20$
将$a+b=2m+1$,$ab=m^{2}+m$代入得:
$2(2m+1)^{2}+(m^{2}+m)=20$
整理得:$2(4m^{2}+4m+1)+m^{2}+m=20$
$8m^{2}+8m+2+m^{2}+m-20=0$
$9m^{2}+9m-18=0$
即$m^{2}+m-2=0$
解得$m_{1}=-2$,$m_{2}=1$
$\therefore m$的值为$-2$或$1$。
23. (8分)问题提出:如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?
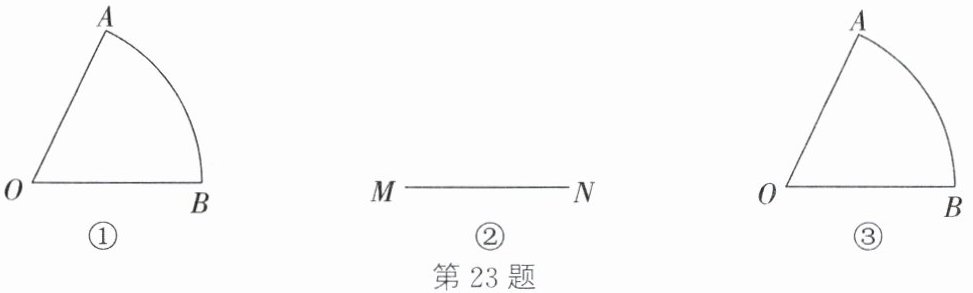
(1)初步尝试:如图①,已知扇形$OAB$,请你用圆规和无刻度的直尺过圆心$O$作一条直线,使扇形的面积被这条直线平分;
(2)问题联想:如图②,已知线段$MN$,请你用圆规和无刻度的直尺作一个以$MN$为斜边的等腰直角三角形$MNP$;
(3)问题再解:如图③,已知扇形$OAB$,请你用圆规和无刻度的直尺作一条以点$O$为圆心的圆弧,使扇形的面积被这条圆弧平分。
注:以上作图均不写作法,但需保留作图痕迹。
(1)初步尝试:如图①,已知扇形$OAB$,请你用圆规和无刻度的直尺过圆心$O$作一条直线,使扇形的面积被这条直线平分;
(2)问题联想:如图②,已知线段$MN$,请你用圆规和无刻度的直尺作一个以$MN$为斜边的等腰直角三角形$MNP$;
(3)问题再解:如图③,已知扇形$OAB$,请你用圆规和无刻度的直尺作一条以点$O$为圆心的圆弧,使扇形的面积被这条圆弧平分。
注:以上作图均不写作法,但需保留作图痕迹。

答案:
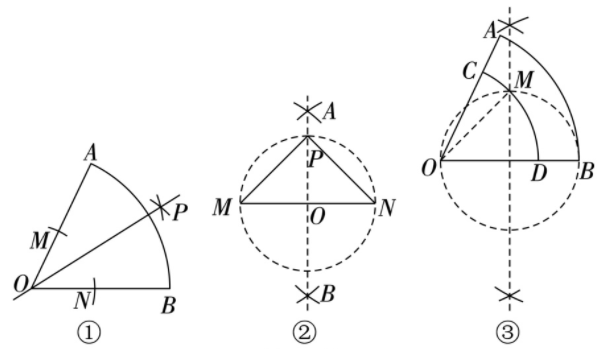

查看更多完整答案,请扫码查看


