18. (6分)已知关于$x$的一元二次方程$2x^{2}+(3m - 2)x - 6 = 0$的两根互为相反数,求$m$的值。
答案:
设方程$2x^{2}+(3m - 2)x - 6 = 0$的两根为$x_1$,$x_2$。
因为两根互为相反数,所以$x_1 + x_2 = 0$。
对于一元二次方程$ax^2 + bx + c = 0$,两根之和$x_1 + x_2 = -\frac{b}{a}$。
在方程$2x^{2}+(3m - 2)x - 6 = 0$中,$a = 2$,$b = 3m - 2$,所以$x_1 + x_2 = -\frac{3m - 2}{2}$。
由$x_1 + x_2 = 0$,得$-\frac{3m - 2}{2} = 0$,
解得$3m - 2 = 0$,$3m = 2$,$m = \frac{2}{3}$。
当$m = \frac{2}{3}$时,原方程为$2x^2 - 6 = 0$,判别式$\Delta = 0^2 - 4×2×(-6) = 48 > 0$,方程有两个不相等的实数根,符合题意。
综上,$m$的值为$\frac{2}{3}$。
因为两根互为相反数,所以$x_1 + x_2 = 0$。
对于一元二次方程$ax^2 + bx + c = 0$,两根之和$x_1 + x_2 = -\frac{b}{a}$。
在方程$2x^{2}+(3m - 2)x - 6 = 0$中,$a = 2$,$b = 3m - 2$,所以$x_1 + x_2 = -\frac{3m - 2}{2}$。
由$x_1 + x_2 = 0$,得$-\frac{3m - 2}{2} = 0$,
解得$3m - 2 = 0$,$3m = 2$,$m = \frac{2}{3}$。
当$m = \frac{2}{3}$时,原方程为$2x^2 - 6 = 0$,判别式$\Delta = 0^2 - 4×2×(-6) = 48 > 0$,方程有两个不相等的实数根,符合题意。
综上,$m$的值为$\frac{2}{3}$。
19. (6分)已知$T=(a + 3b)^{2}+(2a + 3b)(2a - 3b)+a^{2}$。
(1)化简$T$;
(2)若关于$x$的方程$x^{2}+2ax - ab + 1 = 0$有两个相等的实数根,求$T$的值。
(1)化简$T$;
(2)若关于$x$的方程$x^{2}+2ax - ab + 1 = 0$有两个相等的实数根,求$T$的值。
答案:
$(1)$化简$T$
解:
根据完全平方公式$(m+n)^2 = m^2 + 2mn + n^2$,平方差公式$(m+n)(m - n)=m^2 - n^2$对$T=(a + 3b)^{2}+(2a + 3b)(2a - 3b)+a^{2}$进行化简:
对于$(a + 3b)^{2}$,根据完全平方公式可得$(a + 3b)^{2}=a^{2}+6ab + 9b^{2}$;
对于$(2a + 3b)(2a - 3b)$,根据平方差公式可得$(2a + 3b)(2a - 3b)=(2a)^{2}-(3b)^{2}=4a^{2}-9b^{2}$。
将上述结果代入$T$可得:
$\begin{aligned}T&=a^{2}+6ab + 9b^{2}+4a^{2}-9b^{2}+a^{2}\\&=(a^{2}+4a^{2}+a^{2})+6ab+(9b^{2}-9b^{2})\\&=6a^{2}+6ab\end{aligned}$
$(2)$求$T$的值
解:
对于一元二次方程$Ax^{2}+Bx + C = 0(A\neq0)$,其判别式$\Delta=B^{2}-4AC$,当$\Delta = 0$时,方程有两个相等的实数根。
已知方程$x^{2}+2ax - ab + 1 = 0$有两个相等的实数根,其中$A = 1$,$B = 2a$,$C=-ab + 1$,则$\Delta=(2a)^{2}-4×1×(-ab + 1)=0$。
化简$(2a)^{2}-4×1×(-ab + 1)=0$:
$\begin{aligned}4a^{2}+4ab-4&=0\\a^{2}+ab - 1&=0\\a^{2}+ab&=1\end{aligned}$
由$(1)$知$T = 6a^{2}+6ab$,提取公因式$6$可得$T=6(a^{2}+ab)$。
把$a^{2}+ab = 1$代入$T=6(a^{2}+ab)$,得$T = 6×1=6$。
综上,答案依次为:$(1)$$T = 6a^{2}+6ab$;$(2)$$6$。
解:
根据完全平方公式$(m+n)^2 = m^2 + 2mn + n^2$,平方差公式$(m+n)(m - n)=m^2 - n^2$对$T=(a + 3b)^{2}+(2a + 3b)(2a - 3b)+a^{2}$进行化简:
对于$(a + 3b)^{2}$,根据完全平方公式可得$(a + 3b)^{2}=a^{2}+6ab + 9b^{2}$;
对于$(2a + 3b)(2a - 3b)$,根据平方差公式可得$(2a + 3b)(2a - 3b)=(2a)^{2}-(3b)^{2}=4a^{2}-9b^{2}$。
将上述结果代入$T$可得:
$\begin{aligned}T&=a^{2}+6ab + 9b^{2}+4a^{2}-9b^{2}+a^{2}\\&=(a^{2}+4a^{2}+a^{2})+6ab+(9b^{2}-9b^{2})\\&=6a^{2}+6ab\end{aligned}$
$(2)$求$T$的值
解:
对于一元二次方程$Ax^{2}+Bx + C = 0(A\neq0)$,其判别式$\Delta=B^{2}-4AC$,当$\Delta = 0$时,方程有两个相等的实数根。
已知方程$x^{2}+2ax - ab + 1 = 0$有两个相等的实数根,其中$A = 1$,$B = 2a$,$C=-ab + 1$,则$\Delta=(2a)^{2}-4×1×(-ab + 1)=0$。
化简$(2a)^{2}-4×1×(-ab + 1)=0$:
$\begin{aligned}4a^{2}+4ab-4&=0\\a^{2}+ab - 1&=0\\a^{2}+ab&=1\end{aligned}$
由$(1)$知$T = 6a^{2}+6ab$,提取公因式$6$可得$T=6(a^{2}+ab)$。
把$a^{2}+ab = 1$代入$T=6(a^{2}+ab)$,得$T = 6×1=6$。
综上,答案依次为:$(1)$$T = 6a^{2}+6ab$;$(2)$$6$。
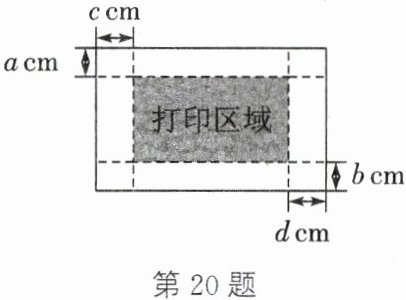
20. (6分)如图,在打印图片之前,为确定打印区域,需设置纸张大小和页边距(纸张的边线到打印区域的距离),上、下、左、右的页边距分别为$a\mathrm{cm}$、$b\mathrm{cm}$、$c\mathrm{cm}$、$d\mathrm{cm}$。若纸张大小为$16\mathrm{cm}×10\mathrm{cm}$,考虑到整体的美观性,要求各页边距相等并使打印区域的面积占纸张的$70\%$,则需如何设置页边距?

答案:
设页边距为 $x$ cm,则打印区域的长为 $(16 - 2x)$ cm,宽为 $(10 - 2x)$ cm。
根据题意,打印区域的面积占纸张面积的 $70\%$,即:
$(16 - 2x)(10 - 2x) = 16 × 10 × 0.7$,
展开并整理得:
$160 - 32x - 20x + 4x^2 = 112$,
$4x^2 - 52x + 48 = 0$,
$x^2 - 13x + 12 = 0$,
通过因式分解法,得:
$(x - 1)(x - 12) = 0$,
解得:
$x_1 = 1, \quad x_2 = 12$,
由于 $x = 12$ 不符合实际情况(页边距过大,打印区域将不存在),所以舍去。
因此,页边距应设置为 $1$ cm。
根据题意,打印区域的面积占纸张面积的 $70\%$,即:
$(16 - 2x)(10 - 2x) = 16 × 10 × 0.7$,
展开并整理得:
$160 - 32x - 20x + 4x^2 = 112$,
$4x^2 - 52x + 48 = 0$,
$x^2 - 13x + 12 = 0$,
通过因式分解法,得:
$(x - 1)(x - 12) = 0$,
解得:
$x_1 = 1, \quad x_2 = 12$,
由于 $x = 12$ 不符合实际情况(页边距过大,打印区域将不存在),所以舍去。
因此,页边距应设置为 $1$ cm。
查看更多完整答案,请扫码查看


