24. (8分)如图,$AB$是$\odot O$的直径,$AC$是$\odot O$的弦,$D$是$\overset{\frown}{AC}$上一点,$P$是$AB$的延长线上的一点,连接$AD$、$DC$、$CP$.
(1)求证:$∠ADC-∠BAC=90^{\circ}$;
(2)若$∠ACP=∠ADC$,$\odot O$的半径为3,$CP=4$,求$AP$的长.
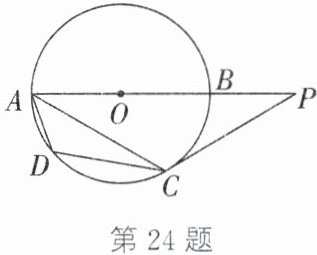
(1)求证:$∠ADC-∠BAC=90^{\circ}$;
(2)若$∠ACP=∠ADC$,$\odot O$的半径为3,$CP=4$,求$AP$的长.

答案:
(1)见证明过程;(2)8。
25. (10分)如图,在$\triangle ABC$中,$AB=AC$,以$AB$为直径的$\odot O$交边$AC$于点$D$,连接$BD$,过点$C$作$CE// AB$.
(1)请用无刻度的直尺和圆规作图:过点$B$作$\odot O$的切线,交$CE$于点$F$(不写作法,保留作图痕迹,标明字母);
(2)在(1)的条件下,求证:$BD=BF$.
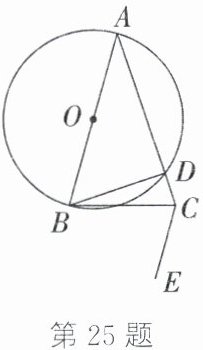
(1)请用无刻度的直尺和圆规作图:过点$B$作$\odot O$的切线,交$CE$于点$F$(不写作法,保留作图痕迹,标明字母);
(2)在(1)的条件下,求证:$BD=BF$.

答案:
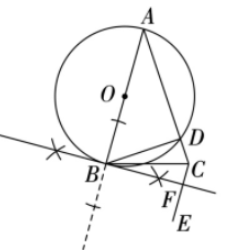
(1)
(2)证明:
∵AB=AC,
∴∠ABC=∠ACB。
∵CE//AB,
∴∠ABC=∠ECB(两直线平行,内错角相等),
∴∠ACB=∠ECB,即BC平分∠ACE。
∵AB是⊙O直径,
∴∠ADB=90°(直径所对圆周角是直角),
∴∠BDC=90°。
∵BF是⊙O切线,
∴∠ABF=90°(切线垂直于半径)。
∵CE//AB,
∴∠BFC=∠ABF=90°(两直线平行,内错角相等)。
在△BDC和△BFC中,
$\left\{\begin{array}{l}∠BDC=∠BFC=90°\\∠BCD=∠BCF\\BC=BC\end{array}\right.$
∴△BDC≌△BFC(AAS),
∴BD=BF。
(1)

(2)证明:
∵AB=AC,
∴∠ABC=∠ACB。
∵CE//AB,
∴∠ABC=∠ECB(两直线平行,内错角相等),
∴∠ACB=∠ECB,即BC平分∠ACE。
∵AB是⊙O直径,
∴∠ADB=90°(直径所对圆周角是直角),
∴∠BDC=90°。
∵BF是⊙O切线,
∴∠ABF=90°(切线垂直于半径)。
∵CE//AB,
∴∠BFC=∠ABF=90°(两直线平行,内错角相等)。
在△BDC和△BFC中,
$\left\{\begin{array}{l}∠BDC=∠BFC=90°\\∠BCD=∠BCF\\BC=BC\end{array}\right.$
∴△BDC≌△BFC(AAS),
∴BD=BF。
查看更多完整答案,请扫码查看


