19. (14分)为加强体育锻炼,增强学生体质,某校在“阳光体育一小时”活动中组织九年级学生定点投篮技能测试,每人投篮4次,投中一次计1分.随机抽取m名学生的成绩作为样本,将收集的数据整理并绘制成如下的统计图表.
测试成绩频数分布表
根据以上信息,解答问题:
(1)请求出m、n的值和样本的众数;
(2)若该校九年级有900名学生参加测试,估计得分超过2分的学生人数.
测试成绩扇形统计图

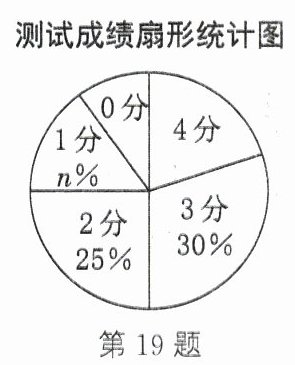
测试成绩频数分布表
根据以上信息,解答问题:
(1)请求出m、n的值和样本的众数;
(2)若该校九年级有900名学生参加测试,估计得分超过2分的学生人数.
测试成绩扇形统计图


答案:
(1)由扇形统计图知2分成绩的频数为15,占比25%,则样本容量$ m = \frac{15}{25\%} = 60 $。
3分成绩占比30%,其频数$ a = 60 × 30\% = 18 $。
总频数之和为60,故$ 12 + 18 + 15 + b + 6 = 60 $,解得$ b = 9 $。
1分成绩的百分比$ n\% = \frac{9}{60} × 100\% = 15\% $,则$ n = 15 $。
样本中频数最高的是3分(18次),故众数为3。
(2)得分超过2分的成绩为3分和4分,样本中其频数之和为$ 18 + 12 = 30 $,占比$ \frac{30}{60} = 50\% $。
估计九年级900名学生中,得分超过2分的人数为$ 900 × 50\% = 450 $。
(1)$ m = 60 $,$ n = 15 $,众数为3;
(2)450。
3分成绩占比30%,其频数$ a = 60 × 30\% = 18 $。
总频数之和为60,故$ 12 + 18 + 15 + b + 6 = 60 $,解得$ b = 9 $。
1分成绩的百分比$ n\% = \frac{9}{60} × 100\% = 15\% $,则$ n = 15 $。
样本中频数最高的是3分(18次),故众数为3。
(2)得分超过2分的成绩为3分和4分,样本中其频数之和为$ 18 + 12 = 30 $,占比$ \frac{30}{60} = 50\% $。
估计九年级900名学生中,得分超过2分的人数为$ 900 × 50\% = 450 $。
(1)$ m = 60 $,$ n = 15 $,众数为3;
(2)450。
查看更多完整答案,请扫码查看


